Outline
- Learn to interpret key light curve features
- Gain familiarity with some of the software tools available for modeling microlensing events
- Practice modeling different events
Shapes of Planetary Caustics in various regions of the parameter space
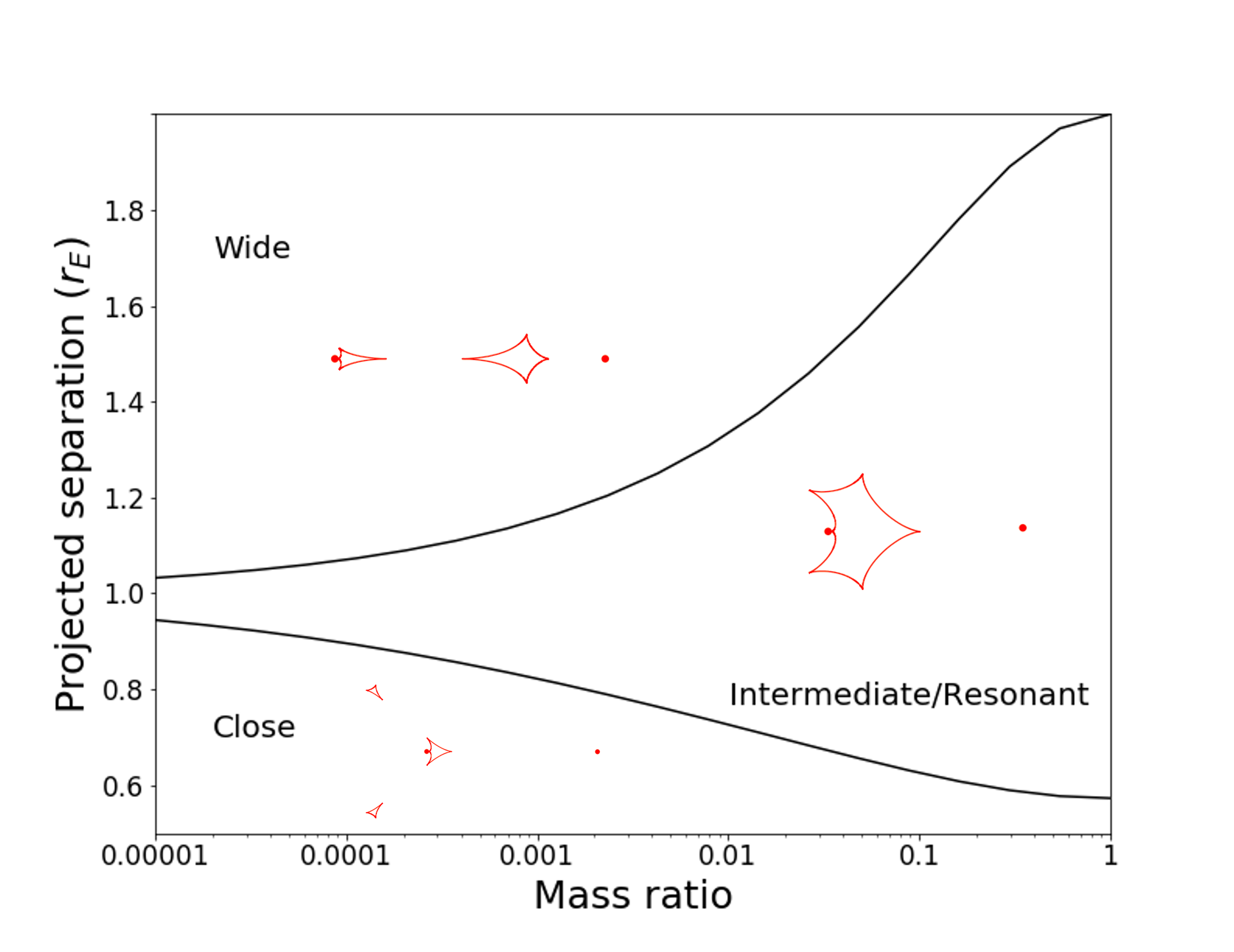
Shapes of Planetary Caustics as a function of projected separation
Gaudi 2021
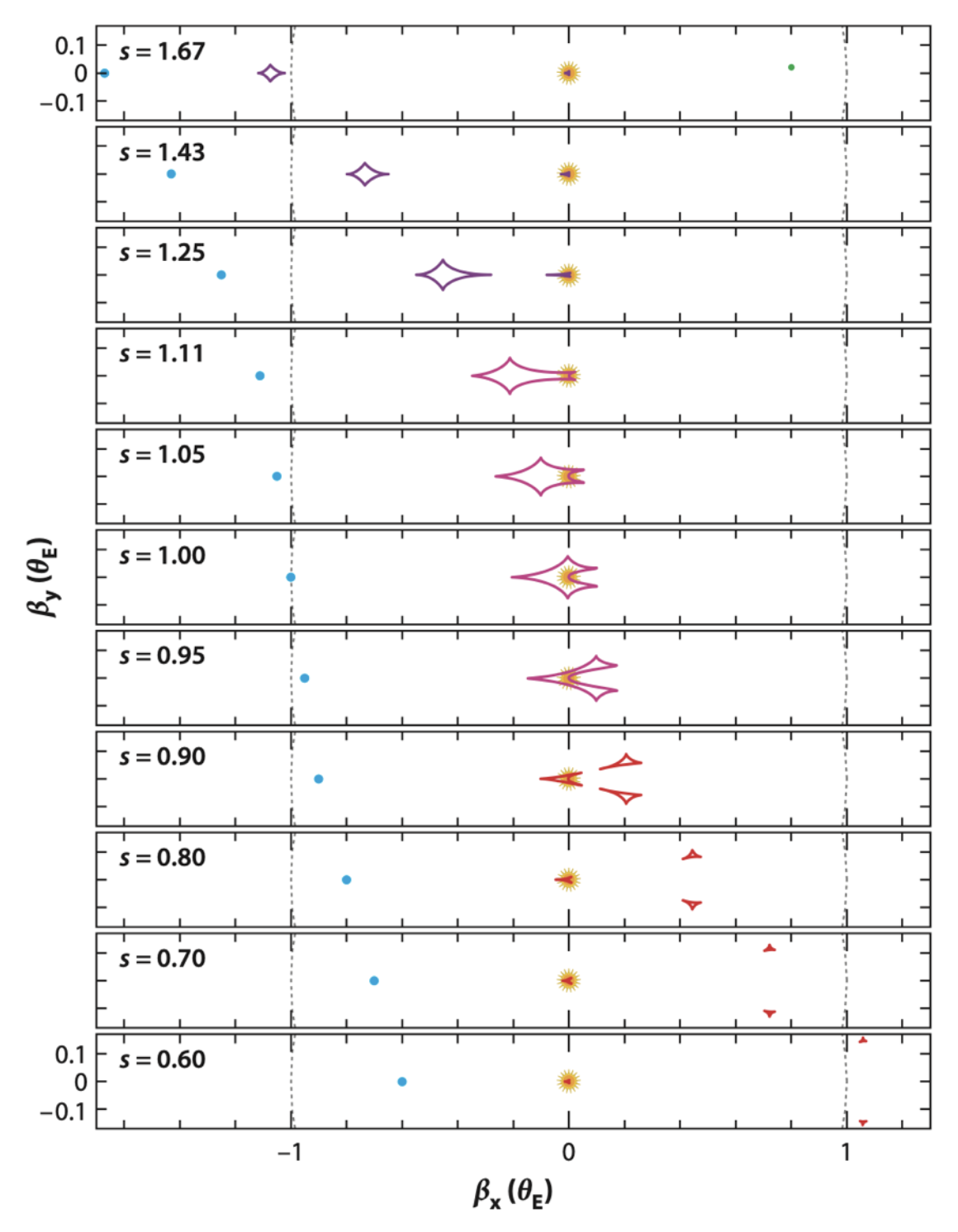
Planetary anomalies in the light curve
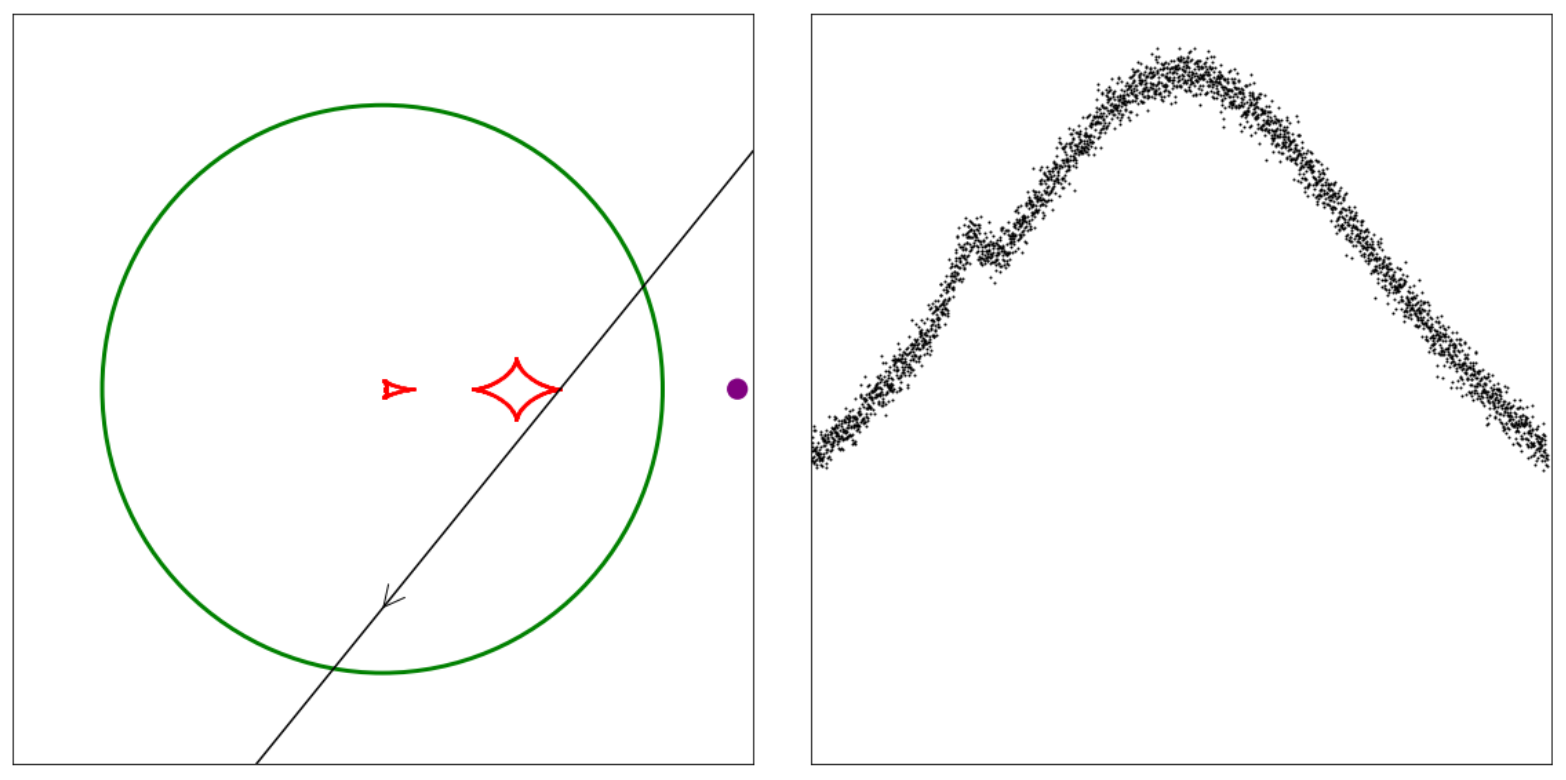
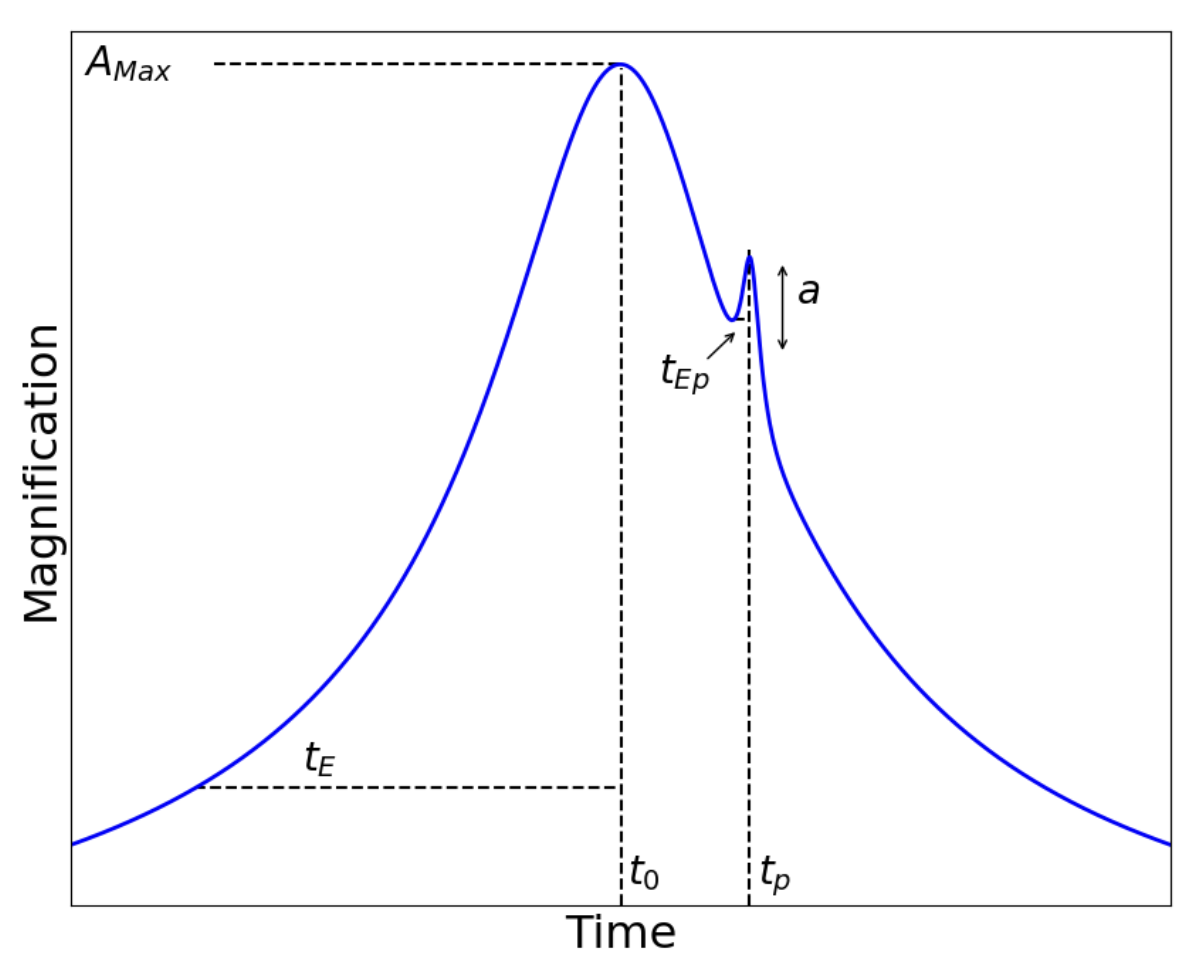
Estimating Planetary Parameters
- Gaudi & Gould (1997) By-eye fitting
- Gould and Loeb (1992)
$$s = \frac{u \pm \sqrt{u^{2} + 4}}{2},$$
where
$$u = \sqrt{u_{0}^{2} + \left(\frac{t_{0}-t_{p}}{t_{E}}\right)^{2}}$$
$$t_{Ep} = \sqrt{(q + \rho^{2})} \times t_{E}, \rho = \frac{t_{*}}{t_{E}}$$
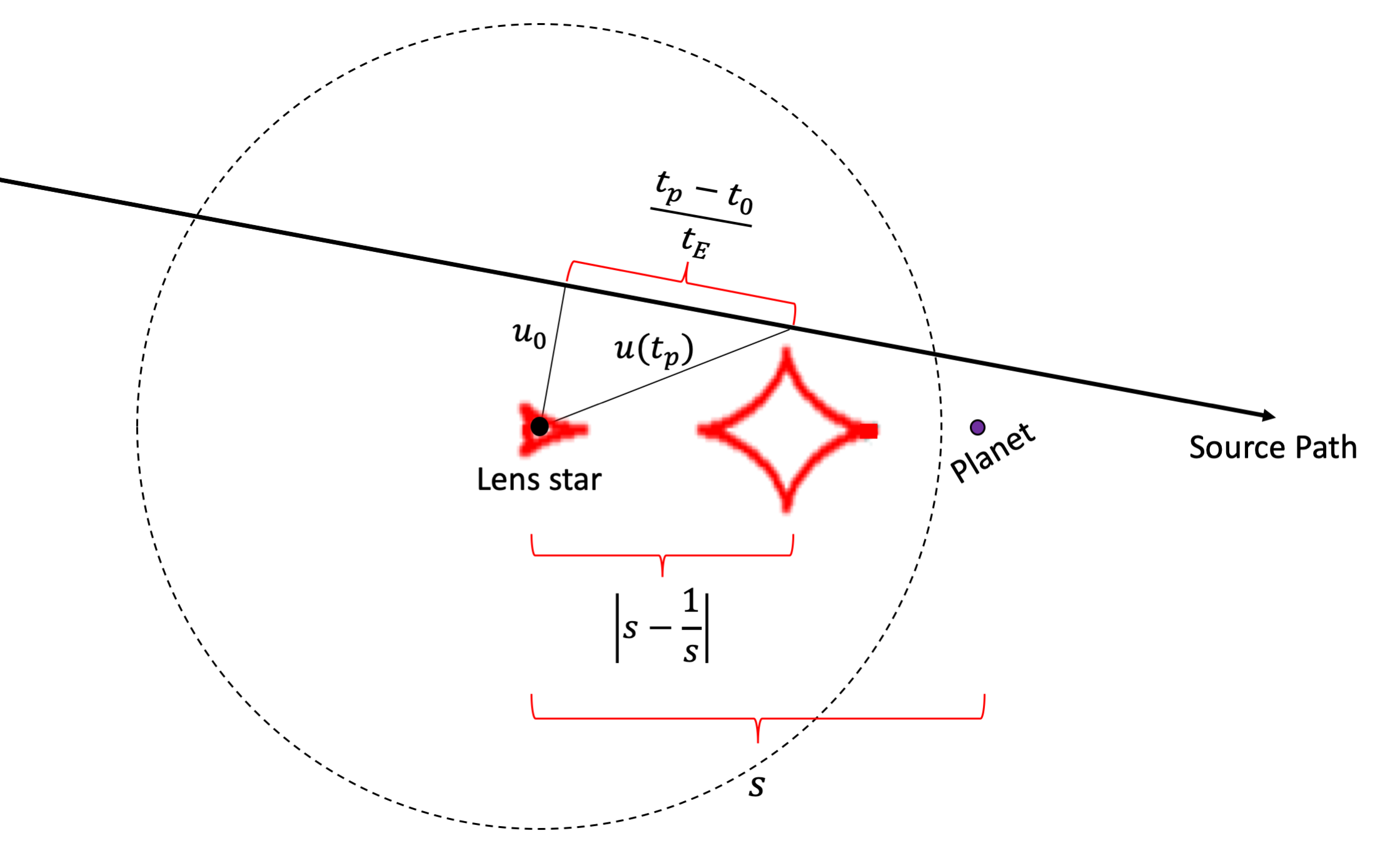
Estimating the Projected Separation
$$u = \sqrt{u_{0}^{2} + \left(\frac{t_{0}-t_{p}}{t_{E}}\right)^{2}}$$
$$s = \frac{u \pm \sqrt{u^{2} + 4}}{2}$$
Minor Image vs Major Image Perturbation
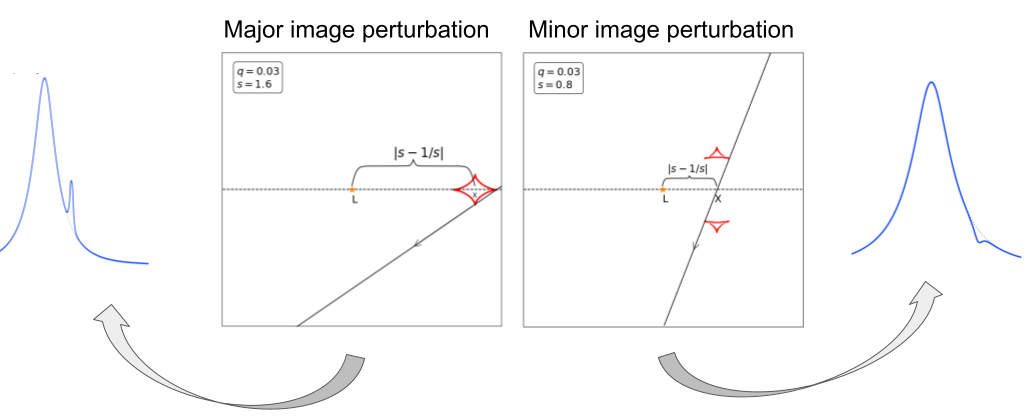
Minor Image vs Major Image Perturbation
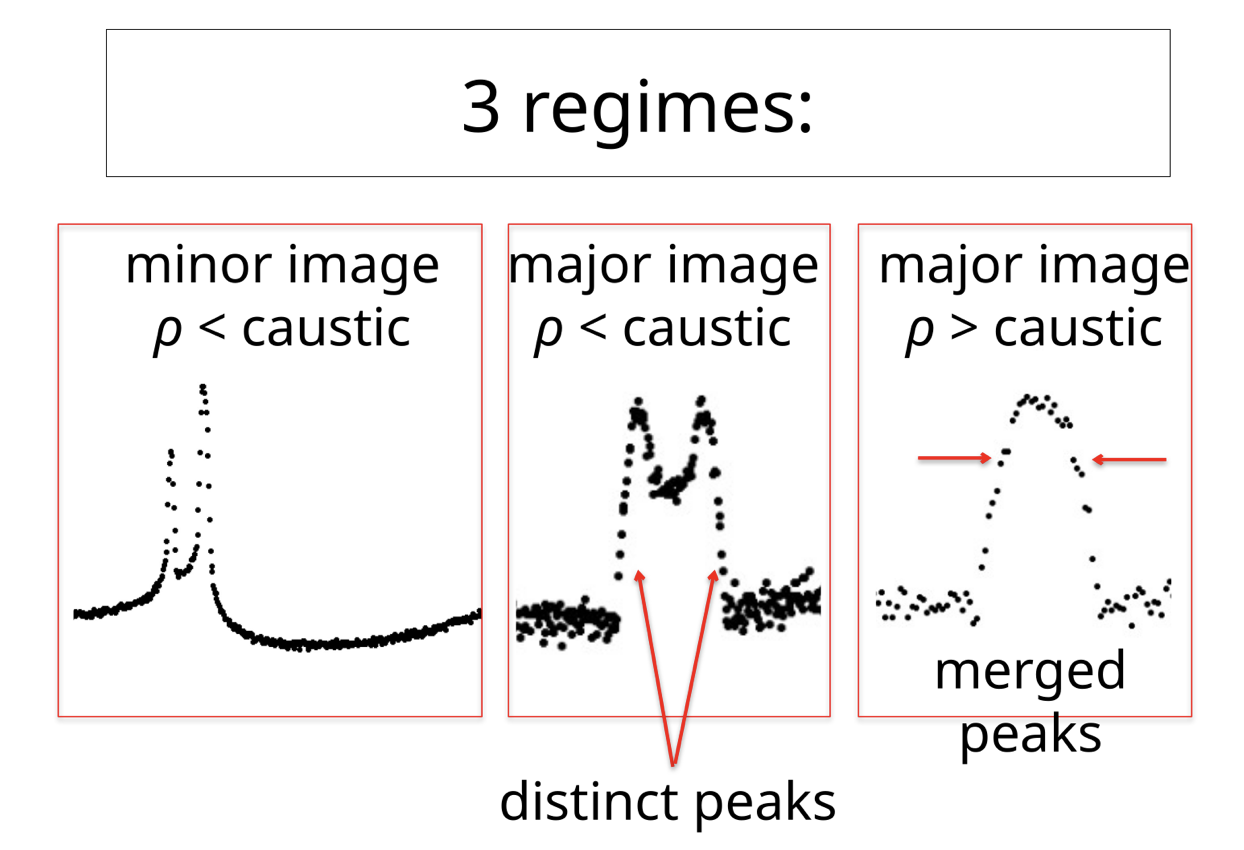
When ρ > caustic
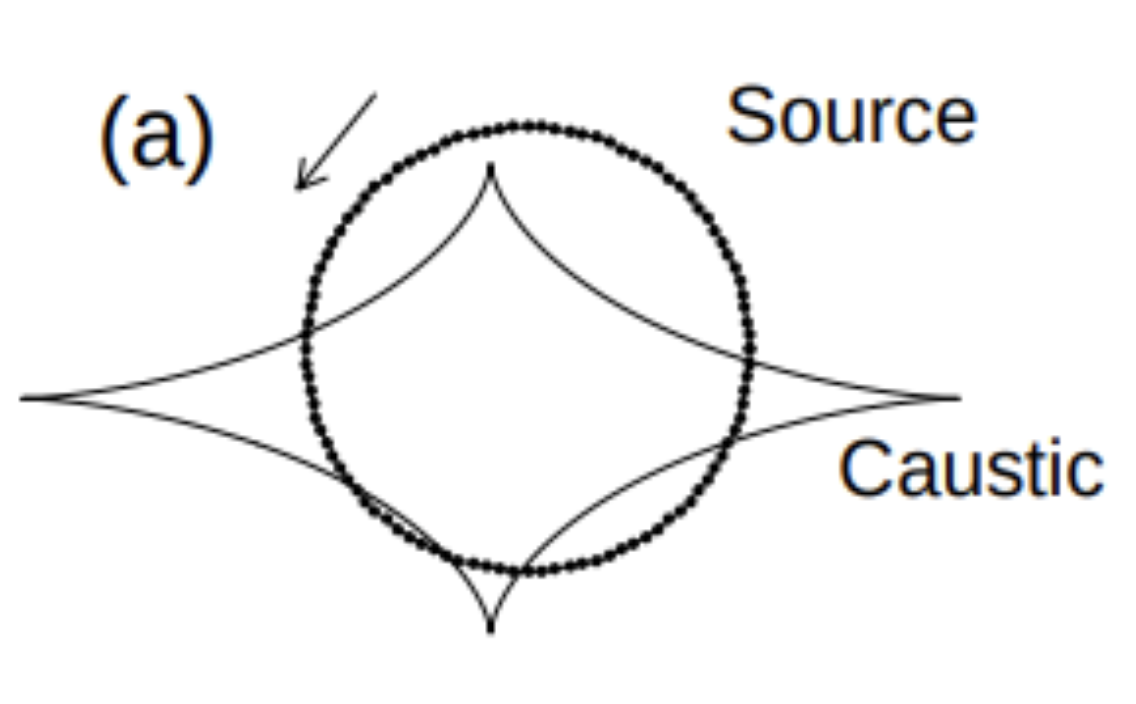
$$\rho = \frac{t_{*}}{t_{E}}$$
Image Gallery
The following images illustrate the light curve features (aka perturbations) corresponding with different source images and caustic structures.
Review these images, then work through the notebooks provided, using the gallery to interpret the light curves in the exercises.
Minor Image Perturbation
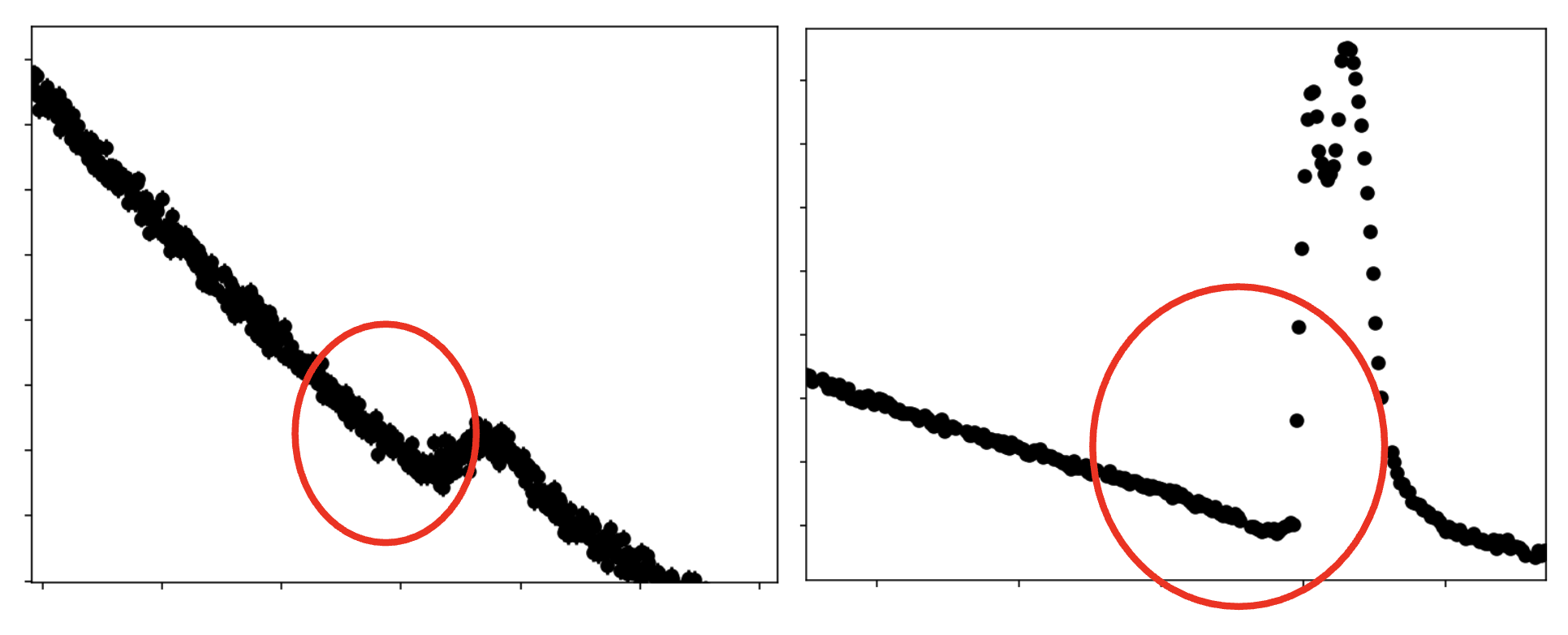
Major Image Perturbation
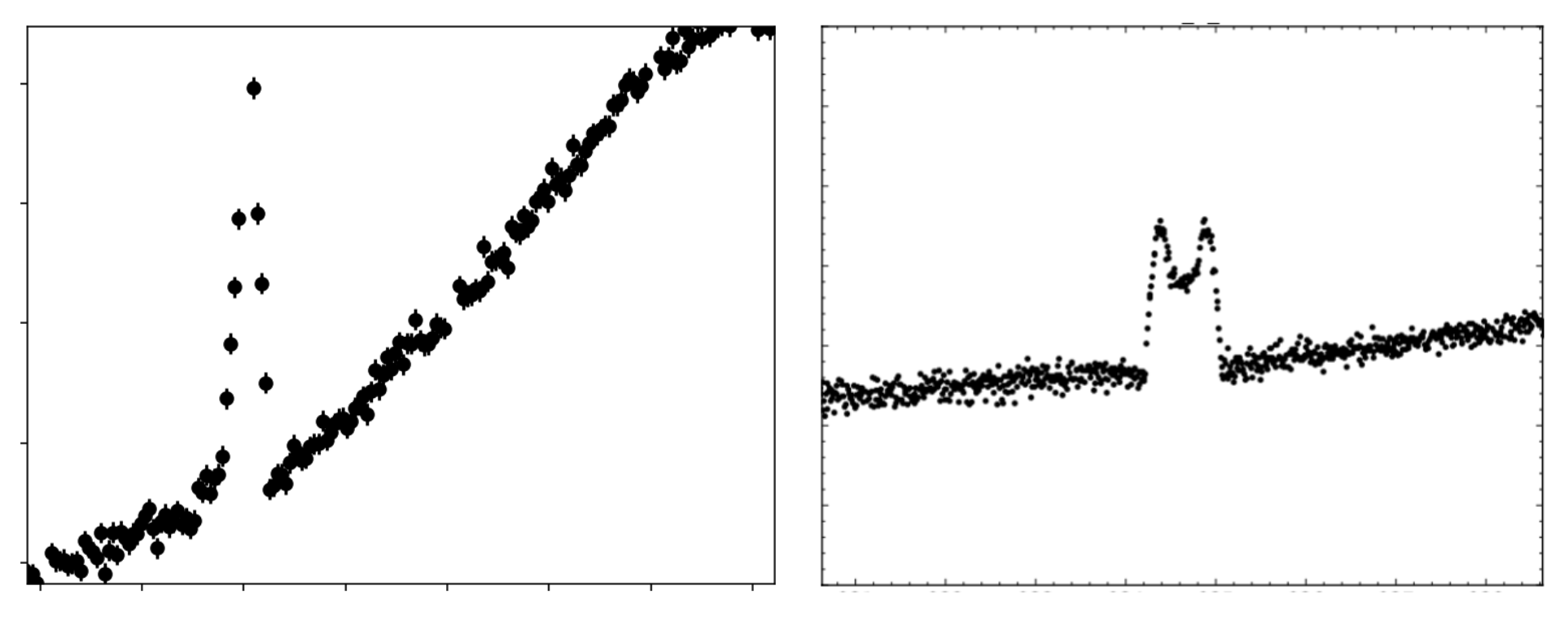
Minor Image, ρ < caustic
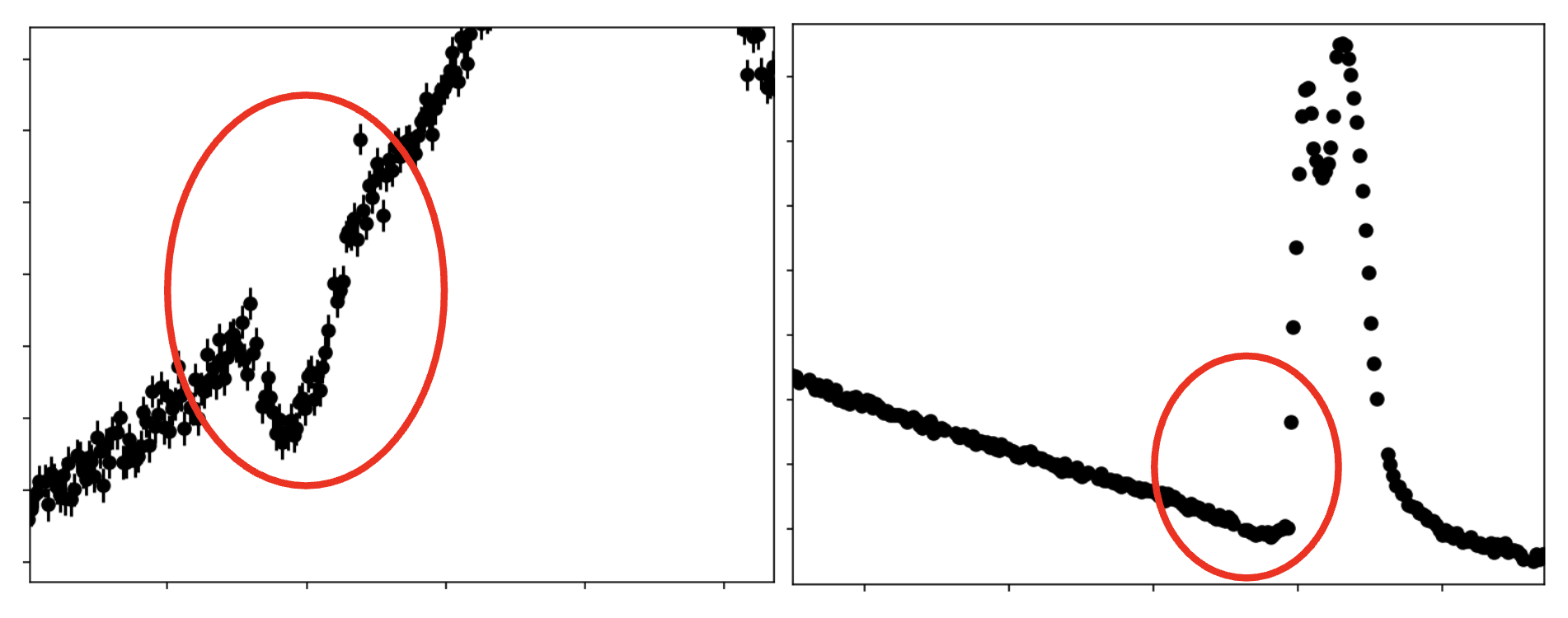
Major Image, ρ < caustic
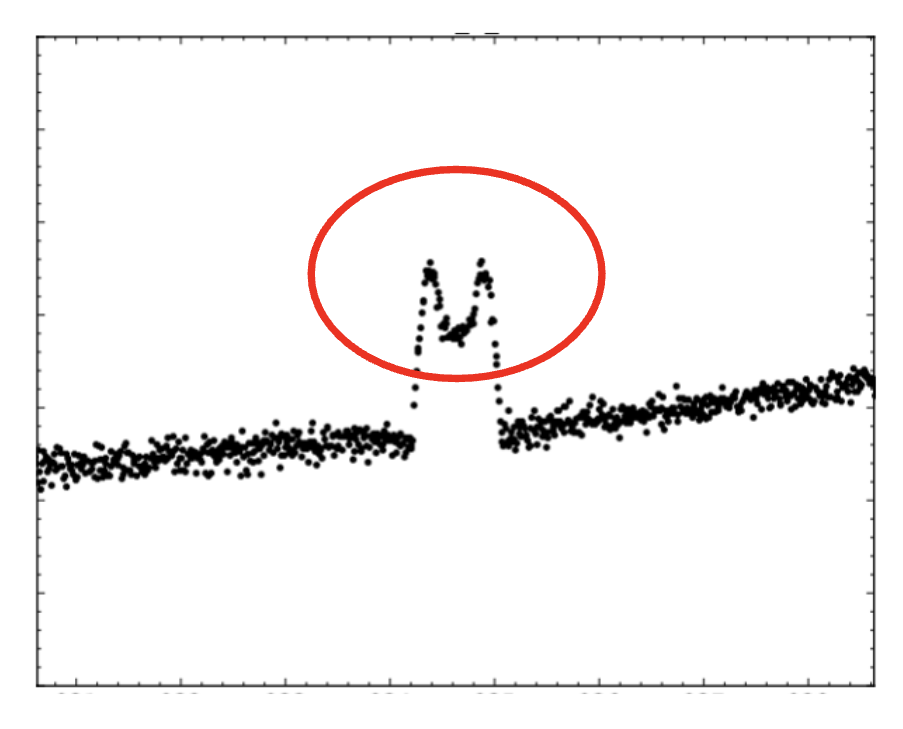
Major Image, ρ > caustic
Notebook Exercises
In order to use them, please make sure you have these packages installed in your environment.