The effects of the physical extend of stars on microlensing
Authors: R.A. Street
Contributors: Y. Tsapras
Introduction
Generally in astronomy its pretty safe to treat them as point sources given their enormous distances!
But microlensing is an extraordinarily sensitive technique and even the radius of a star almost half way across the Galaxy can have a measureable effect.

Image credit: JPL/NASA Solar Dynamic Observatory
Lens and Source Planes
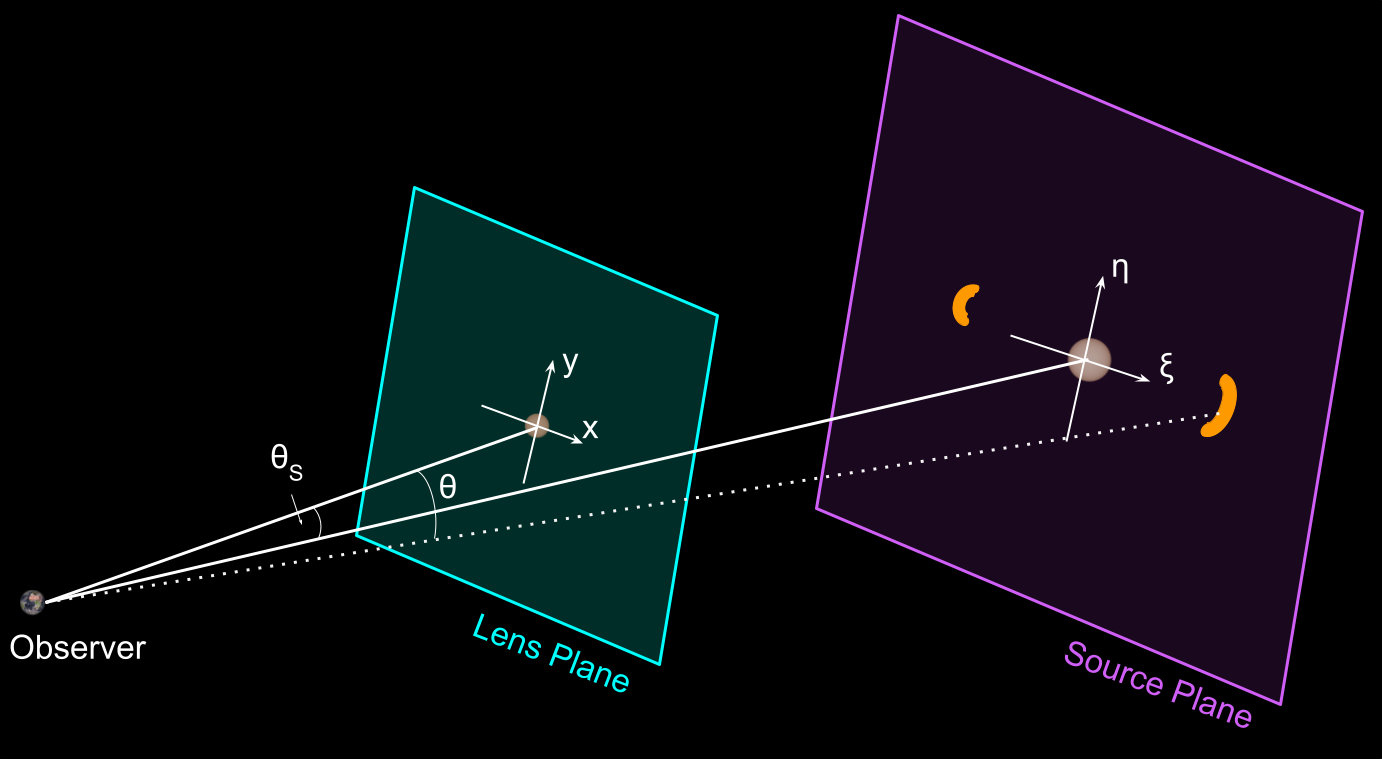
Lensing can be thought of as a 'mapping' of the coordinate system in the lens plane (x,y, centered on the lens) to that of the source (ξ,η).
θ1,2 = angular offsets of source images
θE = angular Einstein radius
θ = angular separation between lens and source
Sources of Finite Extent
Within these reference frames, we need a way to represent the finite disk of the source star, including its radial brightness profile.
RS = source star physical radius
θ* = source star angular radius
ρ = θ* normalized by the angular Einstein radius θE
The Lens Equation (again)
Here we introduce complex notation in order to parameterize the lens equation.
This provides a more natural formulation for two-dimensional vectors. Much of this theory was originally explored in the context of lensed quasars and other large-scale masses.
where z and ζ are normalized to the Einstein radius in the lens, source planes respectively.
The Lens Equation
The equation for a single lens can then be re-written:
where α is the complex deflection angle α(z, z̄) = αx(x, y) + iαy(x, y) and z̄ is the complex conjugate of z.
The solutions of this form of the lens equation are then:
See Witt 1990, Witt & Mao 1994 and Mao & Witt 1998 for a full derivation of finite-source expressions.
Sources of Finite Extent
In this notation a single, circular source of finite radius r can be described as:
where φ = θ-2π and ζ0 is the (parameterized) impact parameter. This is simply substituted into the solutions for the lens equations to derive the parameterized image locations:
Finite Source Size and Magnification
Since surface brightness is conserved, the magnification (Atot) is given by the ratio of the combined image area to that of the unlensed source.
In complex notation the areas of both images is given by:
Finite Source Size and Magnification
In these expressions:
Observable Effects
The observable effects of the finite extent of the source are illustrated below.
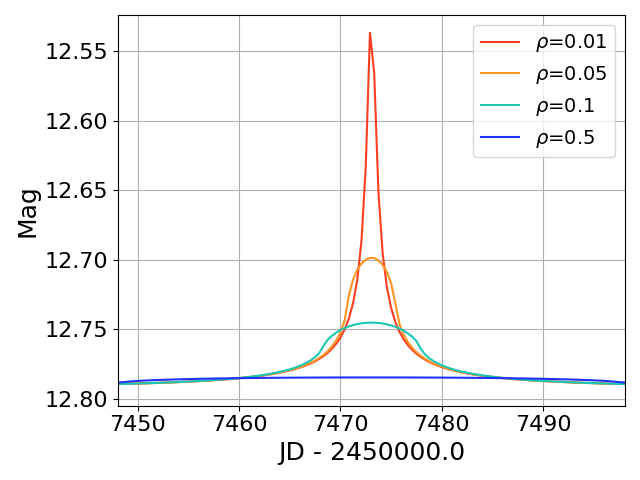
The lightcurve is noticably "rounded-over" at the peak of the event in comparison with the PSPL model, and the amplitude can differ significantly.
These effects become significant when the impact parameter ≈ θ*
In practice this prevents real events from achieving the (theoretical) infinite amplification.
Limb-darkened Finite Sources
The advantage of expressing the lens and amplification equations this way is that it makes it relatively straightforward to introduce one last consideration for a finite source – limb darkening.

Most stars don't have a constant brightness profile over the disk; the intensity drops towards the limb.
Limb darkening laws
Mao & Witt (1998) implemented a formulation of limb-darkening law that is widely-used in microlensing:
Iλ(0) = central intensity, Iλ(r) = intensity out to radius r.
- Wavelength- and source stellar properties dependent
- Several limb-darkening laws in use; not all are convenient for microlensing modeling
Limb darkening Coefficients
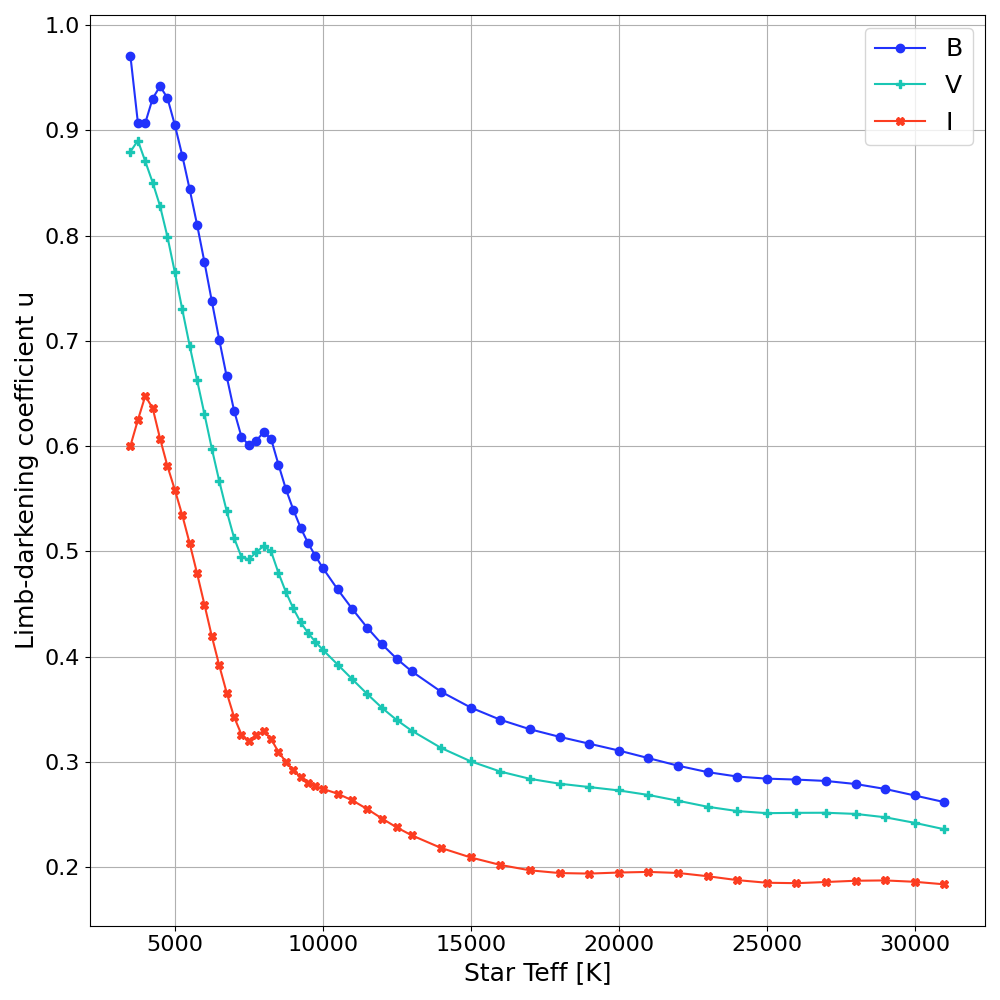
Limb-darkening coefficients appropriate to the passbands used in observations can be found in published tables e.g. Claret et al. 2011. Data on Vizier