What does a microlensing lightcurve look like, and how often do we expect to see microlensing?
Author: Casey Lam
Outline
Review of Lecture 1
Goal 1: Make a microlensing lightcurve
Goal 2: How likely it is to see microlensing?
Review from Chapter 1: the deflection of light
Light is bent (aka deflected) by the presence of mass:
$$\alpha = \frac{4GM}{bc^2}$$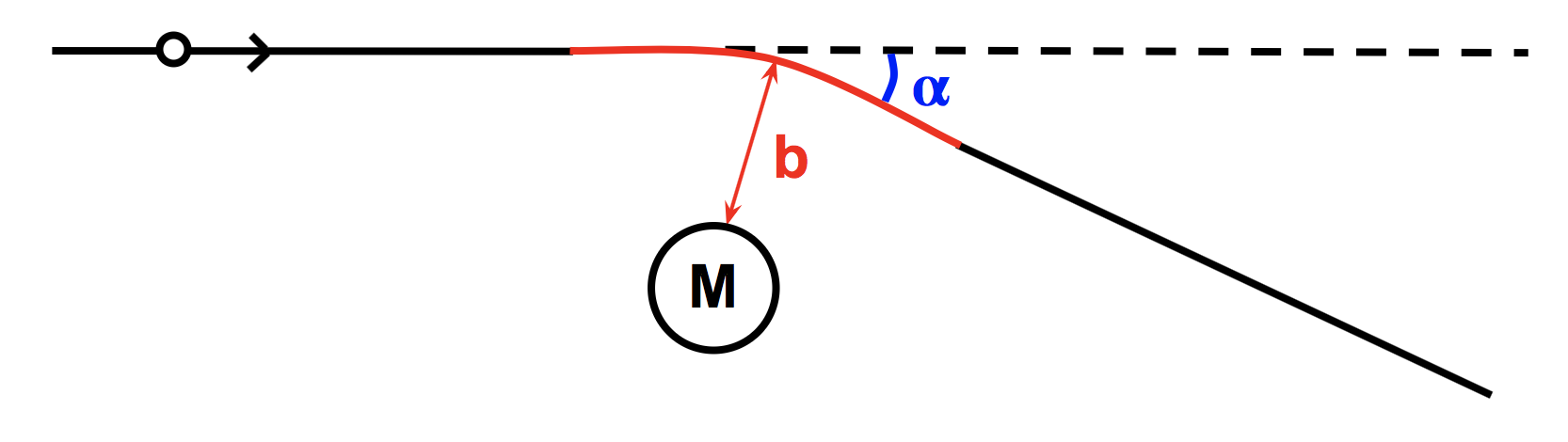
- α = deflection angle
- M = mass of the lens
- b = impact parameter (distance of closest approach)
- G = Newton's gravitational constant
- c = speed of light
More massive lenses (i.e., larger M) = larger deflection angle α.
Light passing closer to the lens M (i.e., smaller b) = larger deflection angle α.
Review from Chapter 1: the lens equation
The lens equation describes where the light looks like it is coming from:
$$\theta^2 - \theta \theta_S - \theta_E^2 = 0, \quad \theta_E \equiv \sqrt{\frac{4GM}{c^2} \left( \frac{1}{D_L} - \frac{1}{D_S} \right)}$$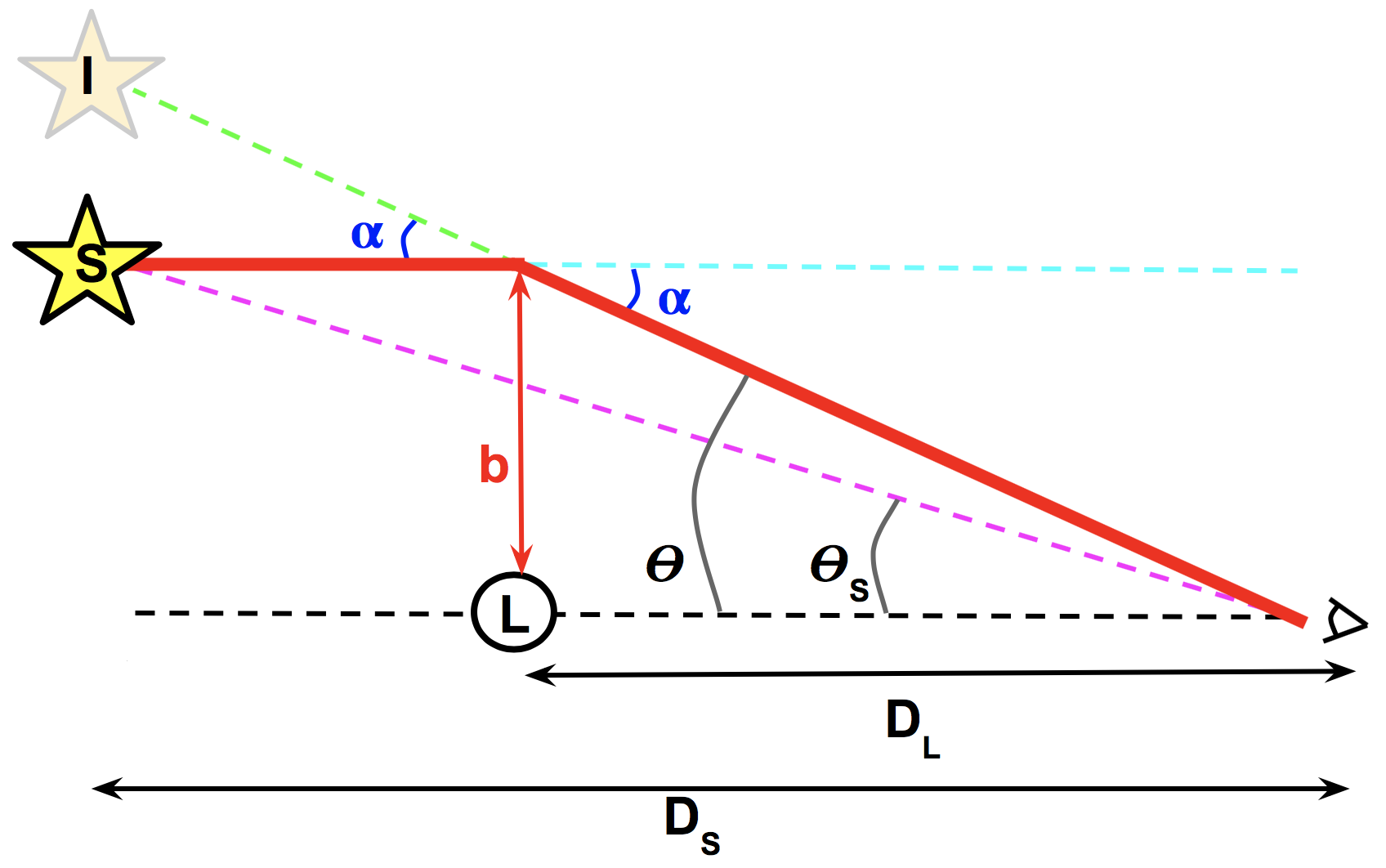
- θ = image position
- θS = background source position
- θE = Einstein radius (characteristic angular scale: depends on lens mass M, observer's distance to the lens DL, source DS)
Goal 1: Make a microlensing lightcurve
- Solving the lens equation
- Connecting the lens equation to magnification
Animation: Scott Gaudi (OSU)
Solving the lens equation
$$\theta^2 - \theta \theta_S - \theta_E^2 = 0$$1) Solve the lens equation for theta using the quadratic formula.
2) Using the result from 1), evaluate theta in the following limits:
a) θS = 0
b) θS << θE
c) θS >> θE
Solving the lens equation
$$\theta^2 - \theta \theta_S - \theta_E^2 = 0$$1) Solve the lens equation for theta using the quadratic formula.
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$Solving the lens equation
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$2) Evaluate theta in the following limits:
$$a) \quad \theta_S = 0 \implies \theta = \theta_E$$ Perfect alignment: an Einstein ring.Solving the lens equation
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$2) Evaluate theta in the following limits:
$$b) \quad \theta_S \ll \theta_E \implies \theta \approx \frac{\theta_S}{2} \pm \theta_E$$ If your source position is within the Einstein radius but not perfectly aligned with the lens, you will get two images: one inside and one outside the Einstein radius.Solving the lens equation
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$2) Evaluate theta in the following limits:
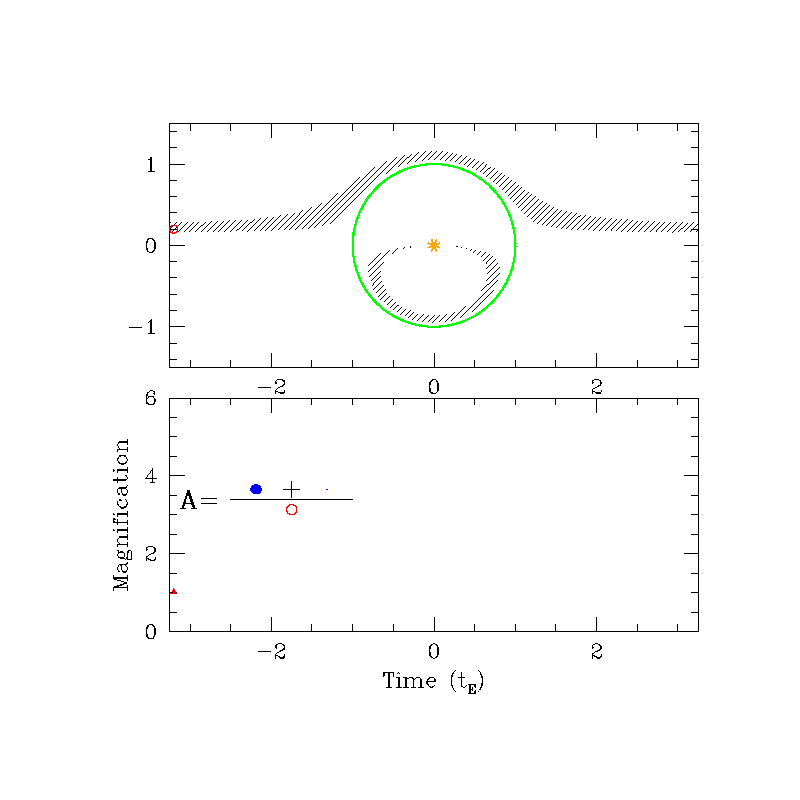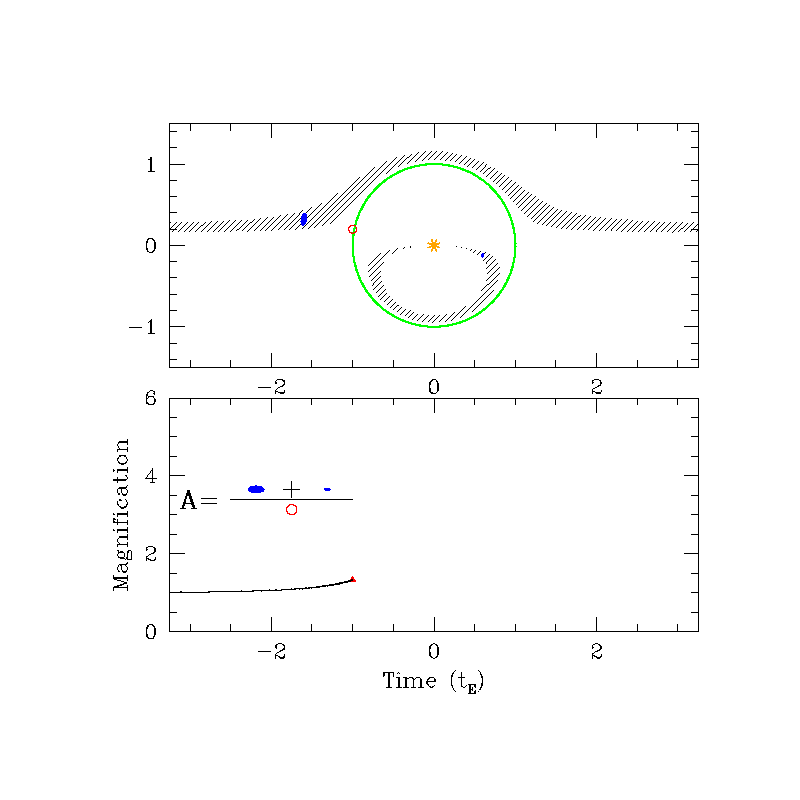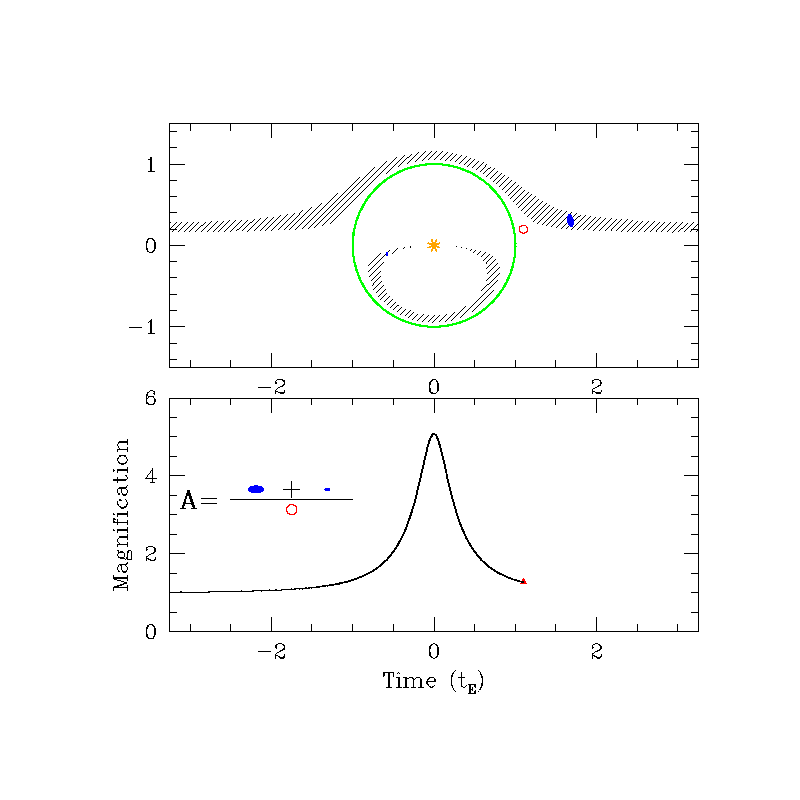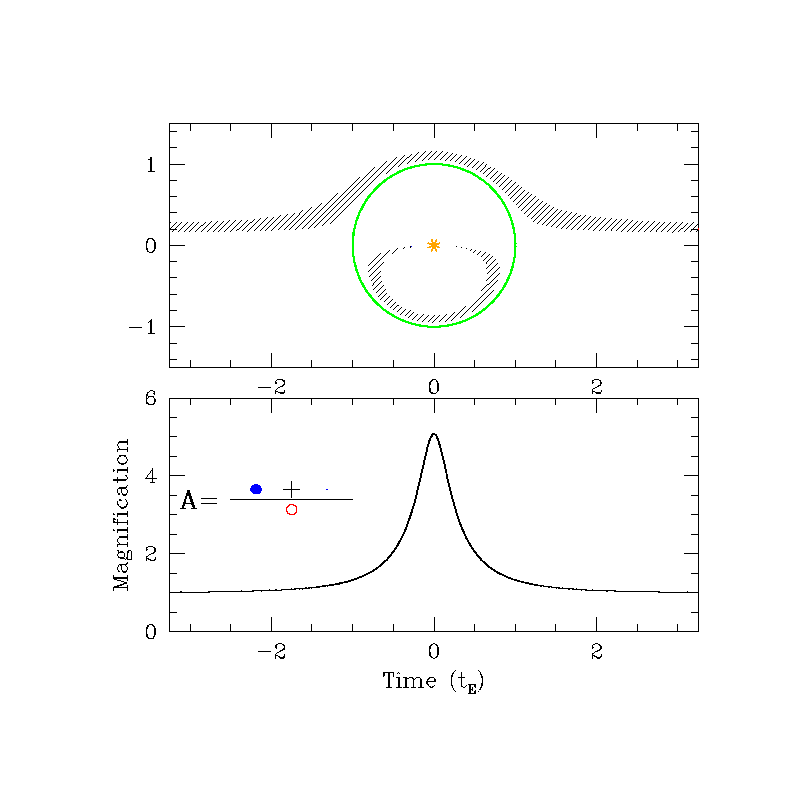
$$c) \quad \theta_S \gg \theta_E \implies \theta \approx 0, \, \theta_S$$ If your source position is much larger than the Einstein radius, you won't have lensingConnecting the lens equation to magnification
Suppose you have four sources located in the same plane (colored circles). The lens is the black dot. The Einstein radius is shown in the dotted line. Qualitatively, sketch where the images of each source would be located.
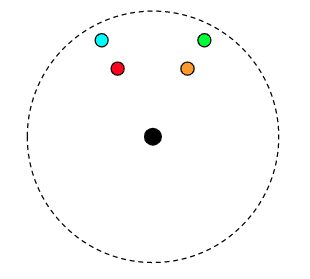
Connecting the lens equation to magnification
Suppose you have four sources located in the same plane (colored circles). The lens is the black dot. The Einstein radius is shown in the dotted line. Qualitatively, sketch where the images of each source would be located.

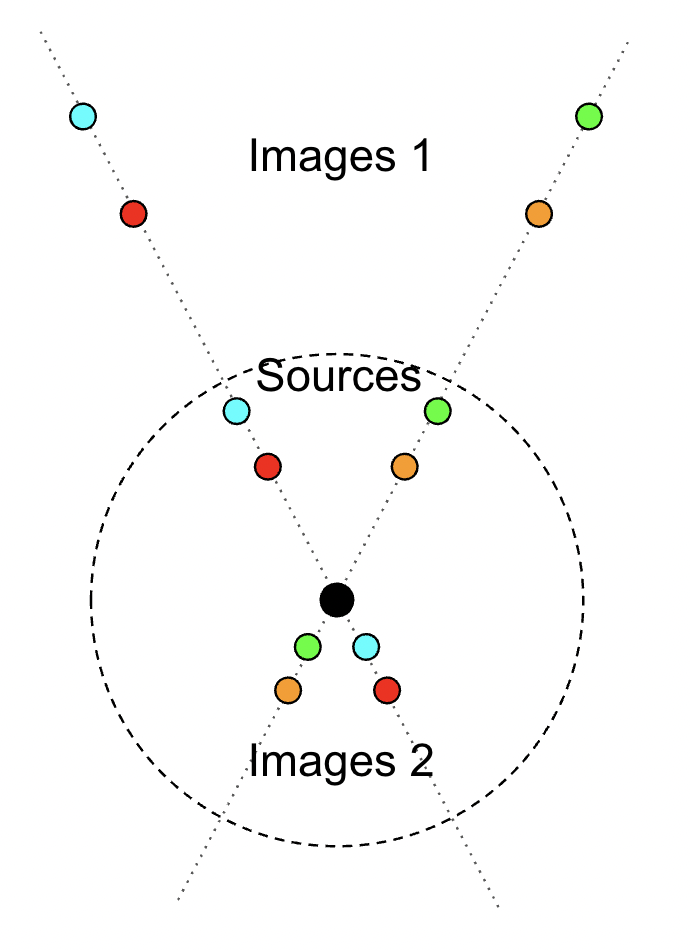
Connecting the lens equation to magnification
Suppose you have four sources located in the same plane (colored circles). The lens is the black dot. The Einstein radius is shown in the dotted line. Qualitatively, sketch where the images of each source would be located.


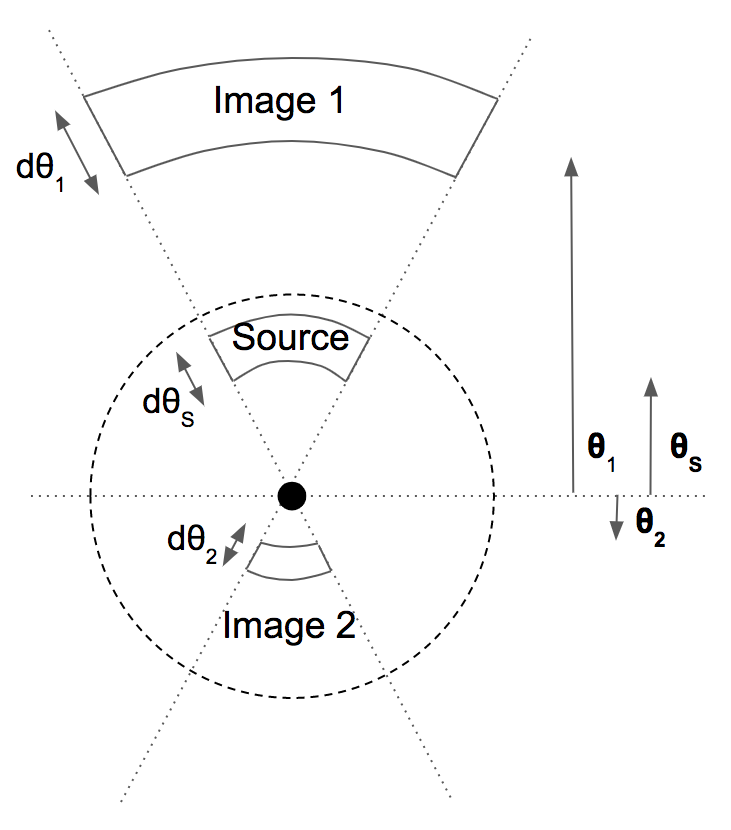
Connecting the lens equation to magnification
Surface brightness is conserved in microlensing: things don't look brighter when you look at them with a magnifying glass.
Then, the ratio of the area of the images to the area of the source A1, A2 is equal to the amount of magnification.
$$A_1 = \frac{\theta_1 \, d\theta_1}{\theta_S \, d\theta_S}, A_2 = \frac{\theta_2 \, d\theta_2}{\theta_S \, d\theta_S}$$
θ1, θ2 are the + and - solutions of the lens equation.
Since there are two images, the total magnification will be the sum of the individual magnifications, A = |A1| + |A2|.
Connecting the lens equation to magnification
If you do the math (differentiate the two solutions of the lens equation wrt θS to calculate what A1 and A2 are), you find the total magnification is:
$$A(u) = \frac{u^2+2}{u\sqrt{u^2+4}}$$where u is the distance of the source from the lens in units of the Einstein radius (dimensionless source-lens projected separation)
$$u \equiv \theta_S/\theta_E$$Making a microlensing lightcurve
A(u) is the equation describing how magnification changes with the dimensionless source-lens projected separation u, but to make a lightcurve we need to know how u as a function of time t:
$$u(t) = \sqrt{u_0^2 + \left( \frac{t - t_0}{t_E} \right)^2}$$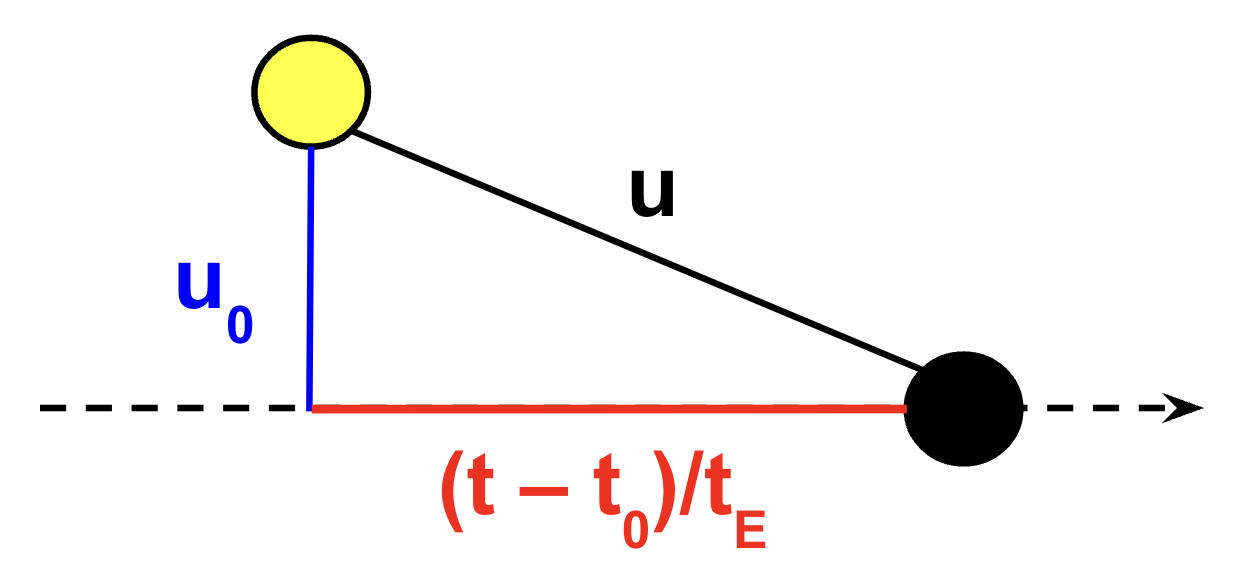
- tE = Einstein crossing time (time it takes for the source to move the distance of the Einstein radius)
- t0 = time of closest approach
- u0 = impact parameter (distance of closest approach)
Making a microlensing lightcurve
Let's code it up in Python to prove it works...
Check out this Jupyter notebookGoal 1: Make a microlensing lightcurve
- Solving the lens equation
- Connecting the lens equation to magnification
Animation: Scott Gaudi (OSU)

Complication: microlensing parallax
We used this equation to calculate the dimensionless source-lens projected separation: $$u(t) = \sqrt{u_0^2 + \left( \frac{t - t_0}{t_E} \right)^2}$$However, this is only accurate if the source and the lens are both moving at constant velocity with respect to the observer. If we are observing from Earth, this is not true: Earth is always accelerating since it orbits the Sun!
Complication: microlensing parallax
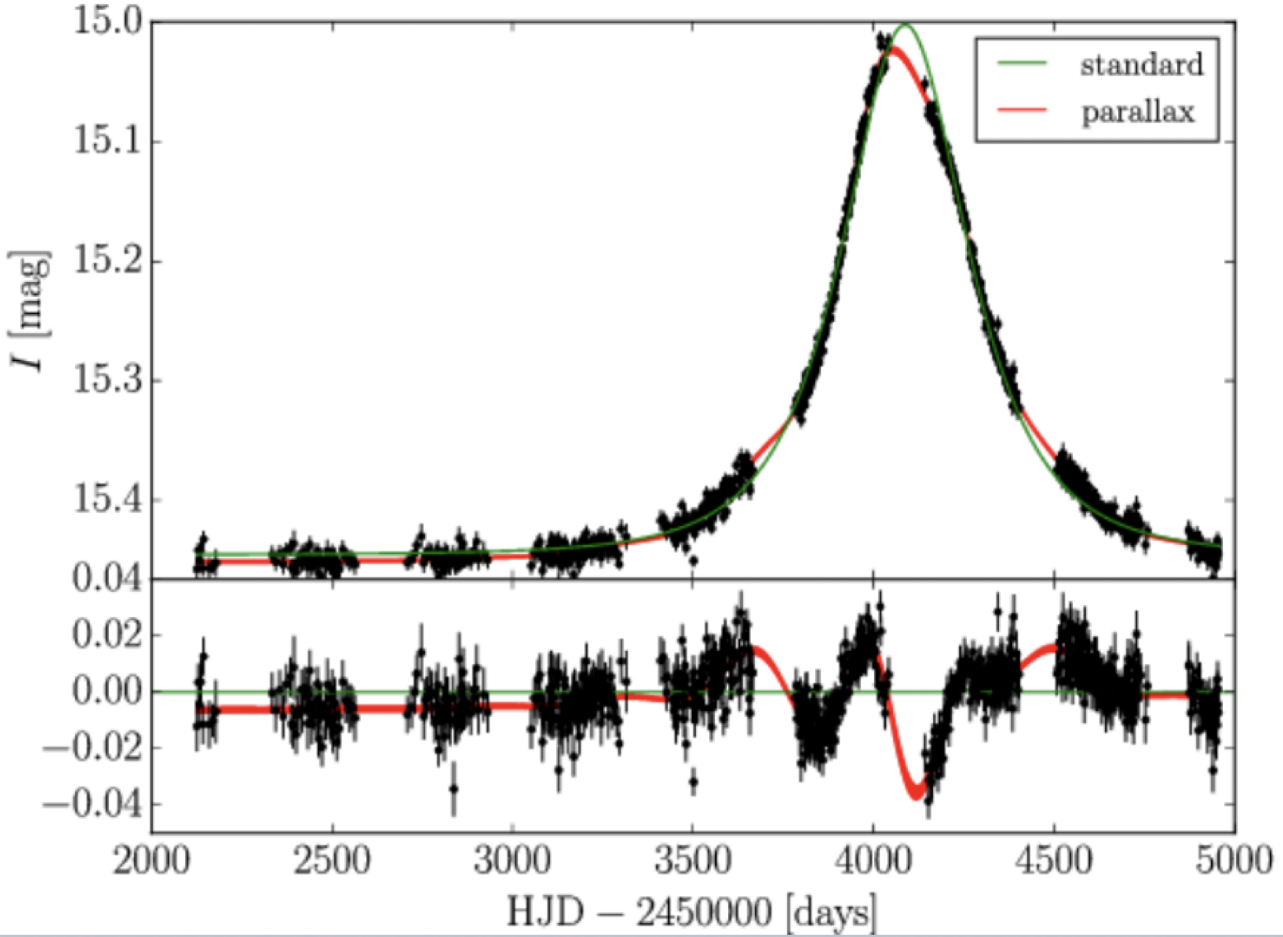
Figure from Wryzykowski et al. 2016
Due to an Earthly observer's accelerating frame, the lightcurve will not be symmetric ("microlensing parallax")
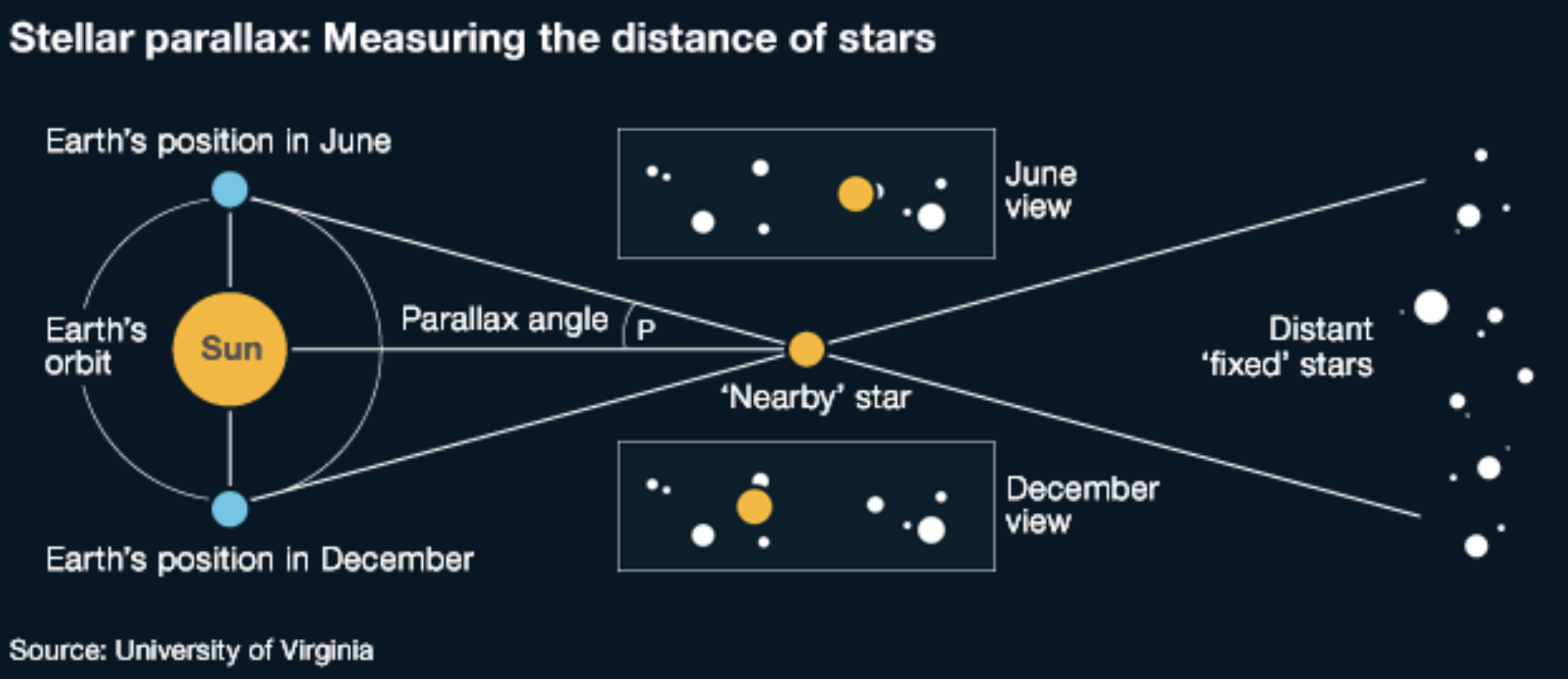
Microlensing parallax is not stellar parallax!
Stellar/trigonometric parallax: the apparent change in position of nearby stars relative to distant background stars, due to Earth orbiting the Sun.
Widely-spaced Observatories
We can only assume that the lensing magnification is the same for all observers if they share the same line of sight to the event.
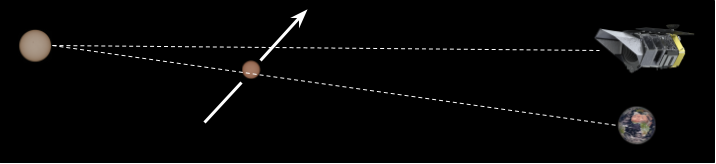
If observers are widely separated (e.g. on Earth and a spacecraft), then the observers will measure different angular separations u at time t.
If this is the case, then we have to take this into account when computing A(u(t)).
Goal 2: How likely it is to see microlensing?
Microlensing optical depth
Microlensing optical depth
Microlensing optical depth is the probability that a star will lie within the Einstein radius of a foreground lens. It describes the distribution of mass along the line of sight of a particular source.
Note: in astronomy, optical depth typically means how transparent a material is to light (high optical depth = opaque, low optical depth = transparent). It has absolutely nothing to do with gravitational lensing.
Microlensing optical depth
ρ(DL) = mass density of lenses
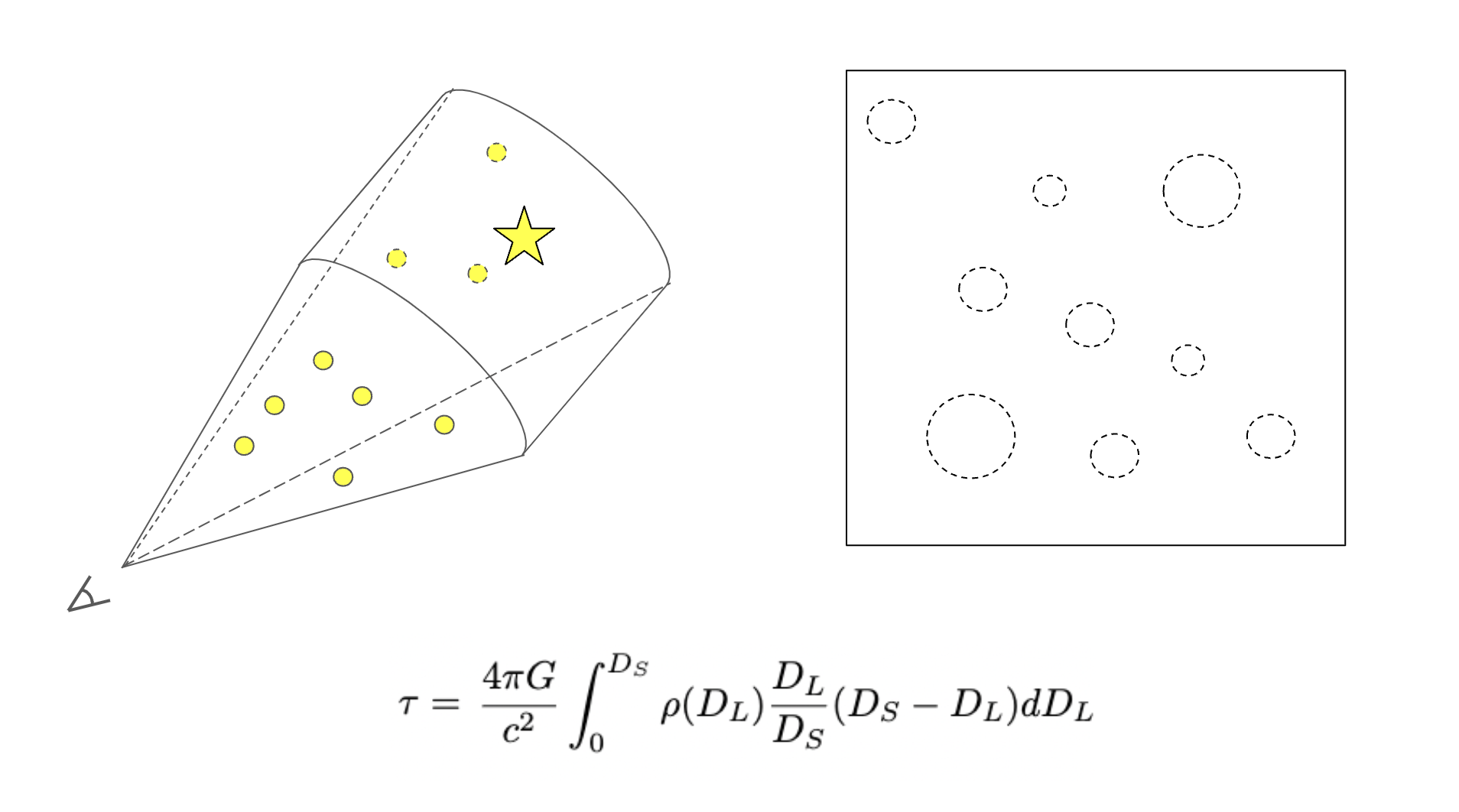
Microlensing optical depth
ρ(DL) = mass density of lenses
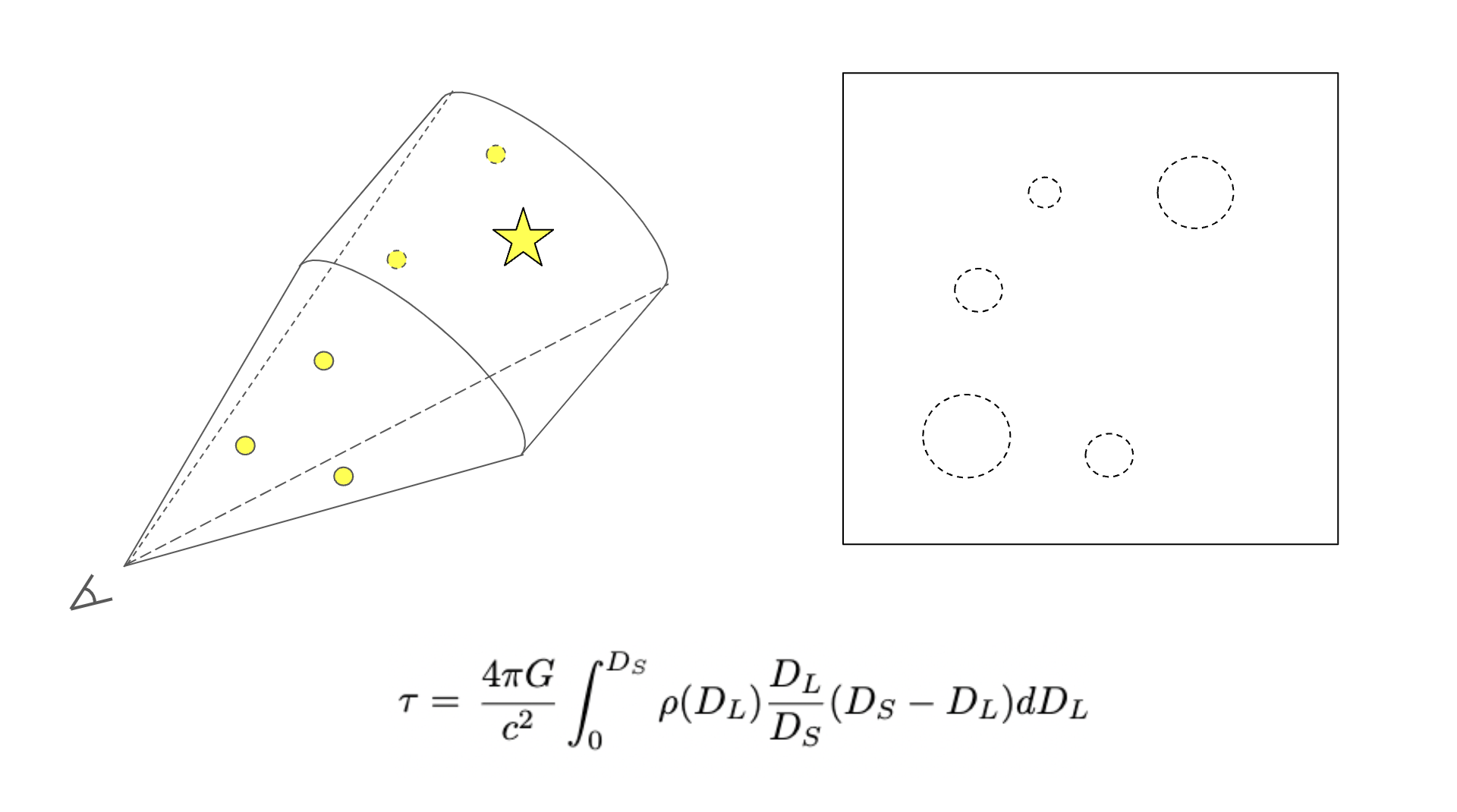
Microlensing optical depth
ρ(DL) = mass density of lenses
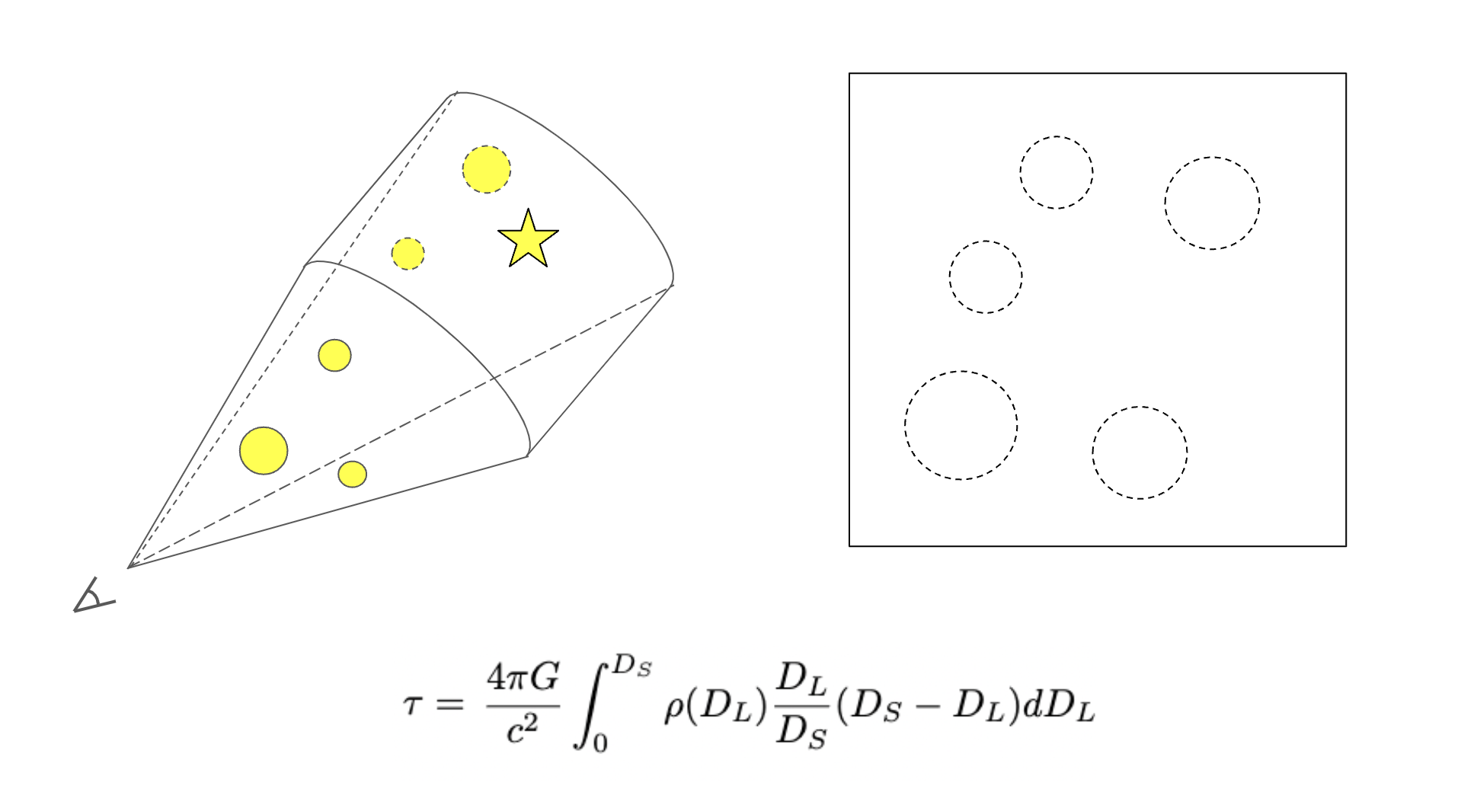
Lensing towards the Bulge: 1 in a million chance
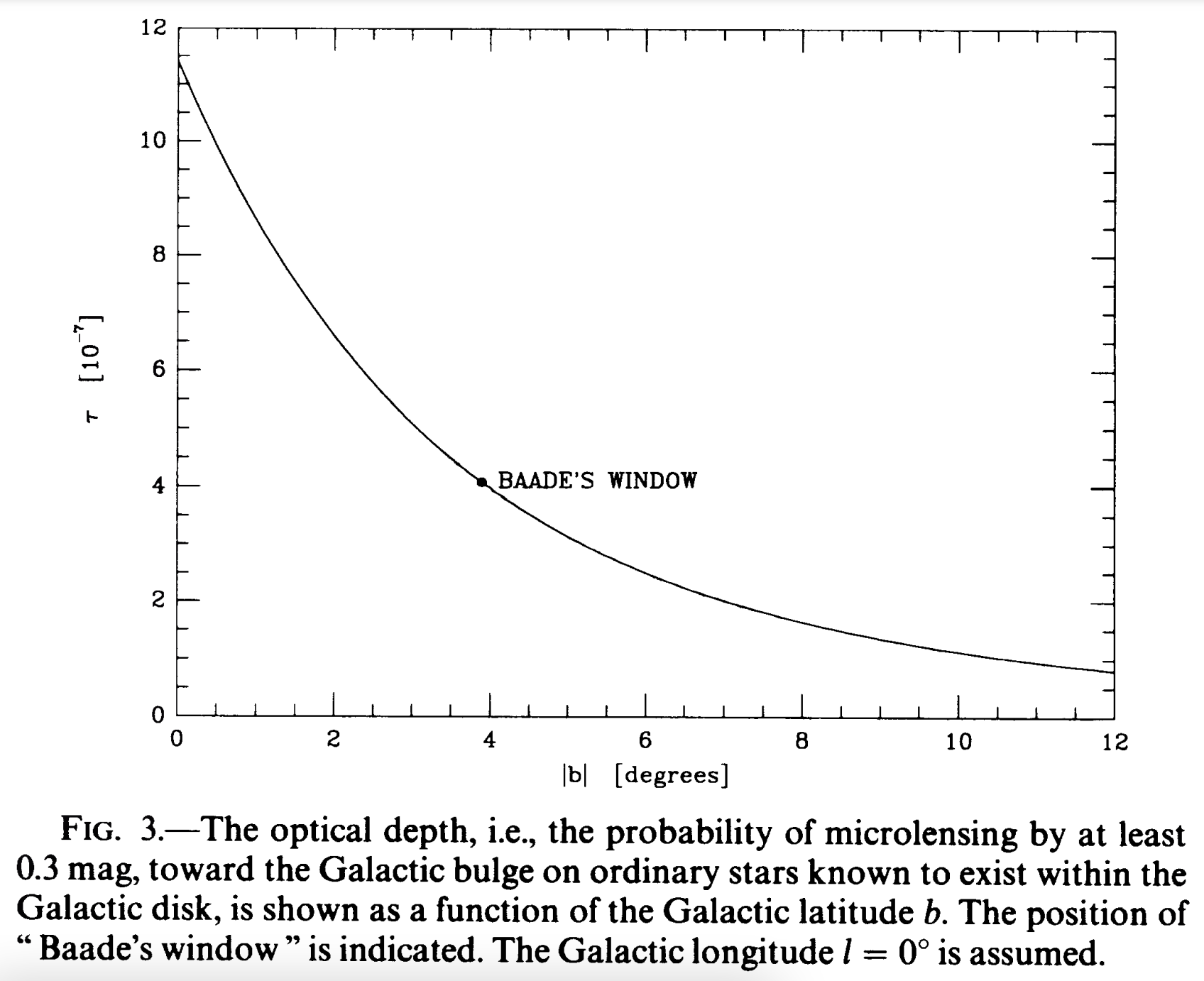

Figure from Paczynski 1991
Microlensing event rate
The microlensing event rate quantifies how often a microlensing event happens:
$$\Gamma = \frac{1}{N_S \Delta T} \sum_i \frac{1}{\varepsilon (t_{E,i})}$$- NS = number of stars monitored
- Δ T = length of survey
- tE,i = detection efficiency, as a function of the Einstein crossing timescale tE
Microlensing optical depth vs. event rate
Both microlensing optical depth and event rate are distinct, but related quantites.- Defined for a specific line of sight and source distance
- Only depends on mass density of lenses along the line of sight
- Units: dimensionless
- Defined for a specific line of sight, integrated over all sources
- Also depends on the velocities of the lenses/sources
- Units: per time (e.g., per year), or per time per angular area (e.g., per year per square degree)