How was gravitational lensing discovered and what are the basics?
Author: Alexander Stephan
Presenter: Scott Gaudi
Outline
1: Early Theories of Light and Gravitational Deflection
2: Einstein's Theories of Relativity
3: Other Lensing Phenomena
4: Lens Equation
1. Early Theory of Light
During Newton's time, the dominant view was that light consisted of "corpuscules", which successfully explained observed phenomena such a polarized light. This "corpuscular theory of light" can be seen as a forerunner of the concept of photons, and originated in the "atomist" view dominant in the natural sciences of the time.
Newtonian Gravitational Lensing
Newtonian physics already predicted that light would be deflected by a gravitational potential. A corpuscule sitting at distance r from a mass M undergoes acceleration
$$\vec{a} = -\frac{GM}{r^2}\hat{r}$$During the interaction, this acceleration results in a velocity boost of
$$\Delta\vec{v} = - \int_{0}^{t_f} \frac{GM}{r(t)^2}\hat{r} \,dt $$Assuming that the corpuscule's closest approach distance is b, and that the light originates far away, the total deflection angle will be
$$\alpha = \frac{2GM}{c^2 b}$$Newtonian Gravitational Lensing, continued
However, we had to assume here that the speed of light is variable and observer dependent, which we now know to be incorrect; as such, the Newtonian prediction is (as we shall see) also incorrect. Nevertheless, the key principle is correct, and it is thus a useful toy model.
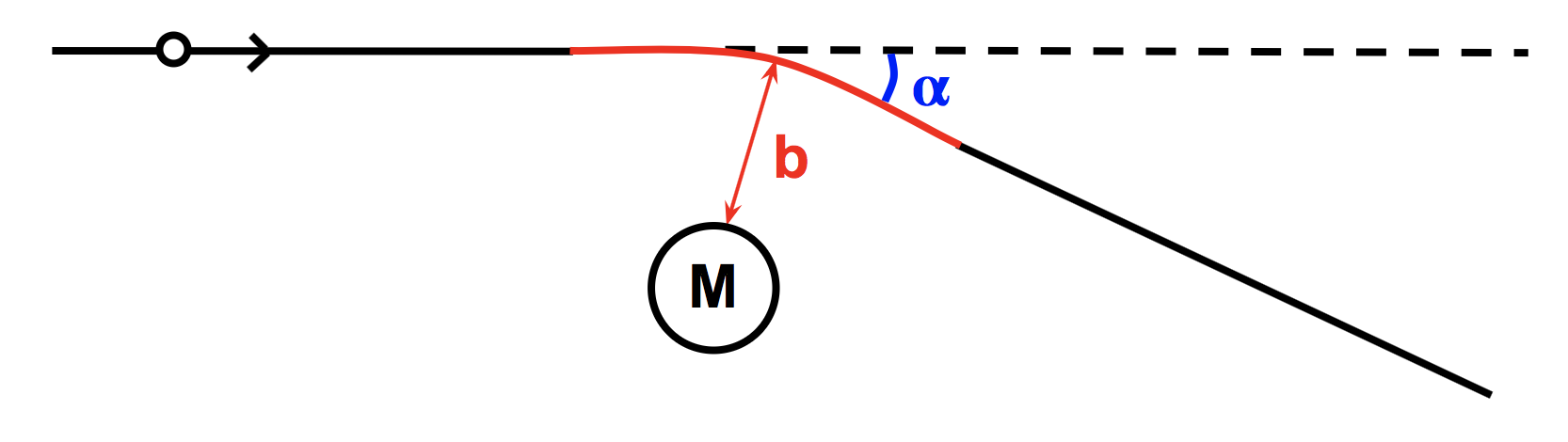
- α = deflection angle
- M = mass of the lens
- b = impact parameter (distance of closest approach)
- G = Newton's gravitational constant
- c = speed of light
More massive lenses (i.e., larger M) = larger deflection angle α.
Light passing closer to the lens M (i.e., smaller b) = larger deflection angle α.
Wave-Particle Duality of Light
The "corpuscular theory of light" was eventually abandoned for the wave theory of light governed by Maxwell's equations. However, as further experiments have shown, light (and all small particles) indeed have wave-particle duality, exhibiting behaviors from both concepts:
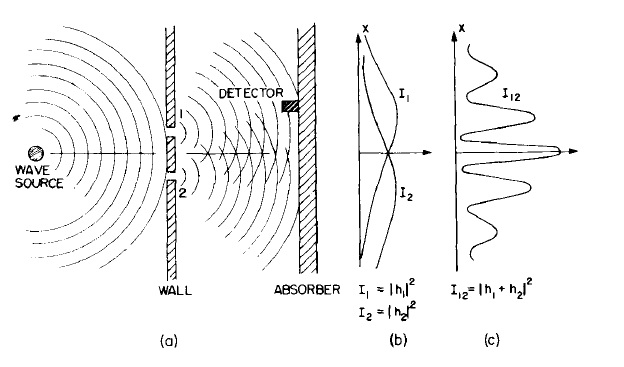
Feynman lecture figure
As light was also determined to be massless, Newtonian gravity should not even affect it at all; as such, the behavior of light under gravity required a new kind of theory.
2. Einstein's Theories of Relativity
In 1905 and 1915, Einstein published his papers that outlined the Special and General Theories of Relativity, respectively. These theories outline a crucial set of assumptions and postulates that still describe our most accurate description of gravity and spacetime:

- constancy of the speed of light for all observers
- laws of physics are the same in all inertial reference frames
- mass-energy equivalency \(E = m c^2\)
- gravity is the result of mass bending spacetime
Einsteinian Gravitational Lensing
Unlike in Newtonian physics, following Einstein's theory of general relativity, gravity is not described as a force, but as the paths of objects following a geodesic, a straight path in curved spacetime. To derive the deflection of a light ray by a point potential \(\Phi\) under GR, we can use the following set of equations (see, for example, Carroll 2004 for a full derivation):
- deflection angle: \(\hat{\alpha} = 2\int\nabla_\perp \frac{\Phi}{c^2} ds \)
- potential: \(\Phi(r) = -\frac{GM}{r} = -\frac{GM}{(b^2 +z^2)^{1/2}} \)
- \(\nabla_\perp \Phi(r) = \frac{\partial \Phi}{\partial b} = -\frac{G M b}{(b^2 +z^2)^{3/2}}\)
- \(z\) is the direction between source and observer
Solving the integral, we get a total deflection angle of: $$\alpha = \frac{4 G M}{c^2 b}$$ This result is exactly twice as large as the deflection angle predicted by Newtonian gravity.
Testing Einstein: Eddington and Dyson (1919)
At the time, it was difficult to test Einstein's gravitational lensing prediction due to the limited capabilities of contemporary instruments. Luckily, the total solar eclipse on May 29th 1919 provided an opportunity to use the sun itself as the gravitational lens. British astronomers Eddignton and Dyson led the expeditions that observed the deflection of light from stars behind the sun and concluded that Einstein's, not Newton's, prediction was correct. Figures reproduced from Eddington's 1920 work:
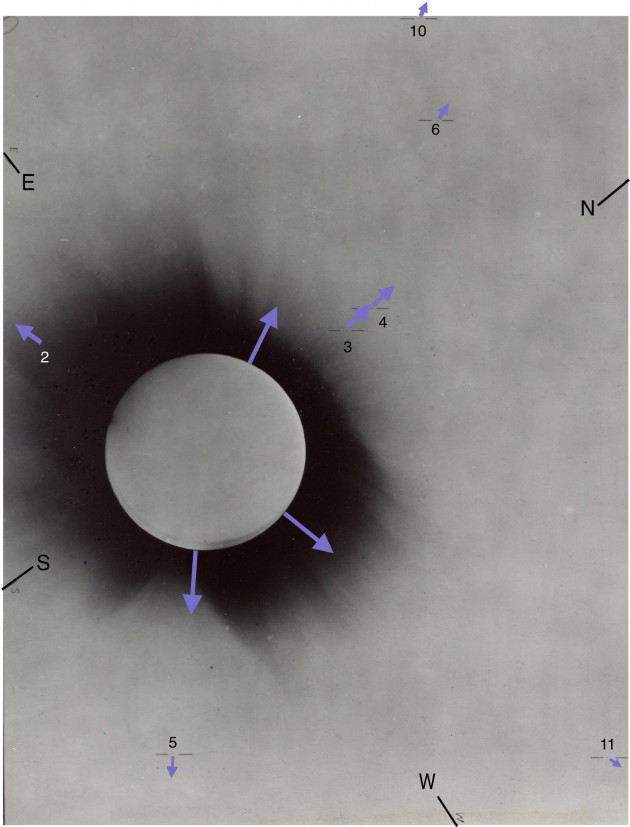
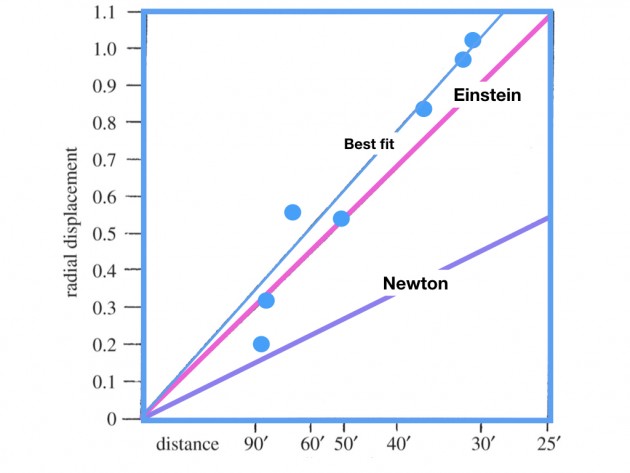
3. Other Lensing Phenomena
Following the establishment of GR and the confirmation of gravitational lensing by Eddington and Dyson, a number of other gravitational lensing phenomena have been predicted, and also observed. Among these are Einstein "crosses" and "rings", where a compact or extended source, respectively, gets lensed multiple times by the foreground lensing mass (Pictures from NASA/ESA/STScl):


Weak Gravitational Lensing
If the lensing mass is not a compact object like a star, but an extended distribution of mass like a galaxy, or a galaxy cluster, the lensing geometry becomes more complex, and multiple image copies with varying levels of distortion and magnification can be observed. This can be helpful to measure the mass distribution of the lensing cluster (Pictures from NASA/ESA/STScl/Hubble):


Microlensing for finding Dark Matter Candidates
While we still do not know what Dark Matter exactly is, early hypotheses included the idea that a large number of unseen massive compact halo objects (MACHOs) exist, detectable via microlensing (Paczyński 1986). Surveys revealed, however, that not enough of these objects exist to explain Dark Matter.
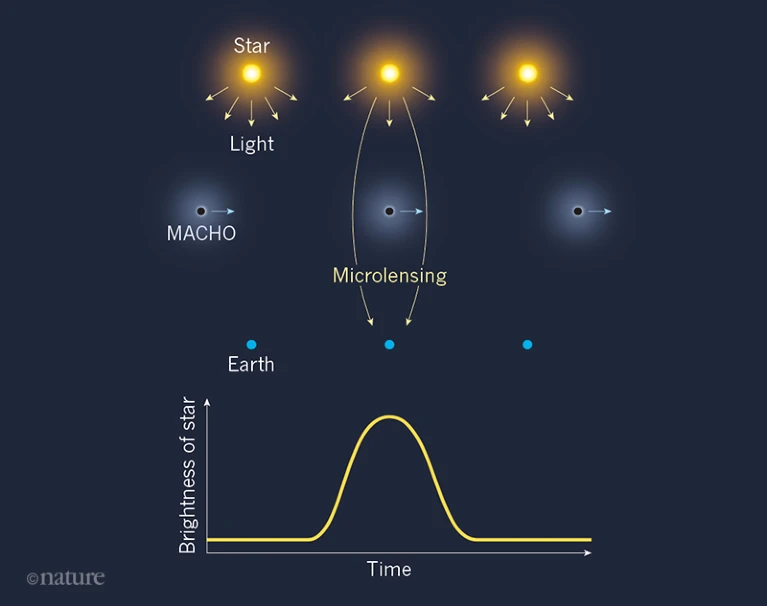
Microlensing for finding Exoplanets
Following the idea that microlensing could be used to find dark compact objects, Gould & Loeb (1992) suggested to use microlensing to detection exoplanets - this detection method has some significant advantages over others, and the rest of the minicourse will focus on the technical details behind it.

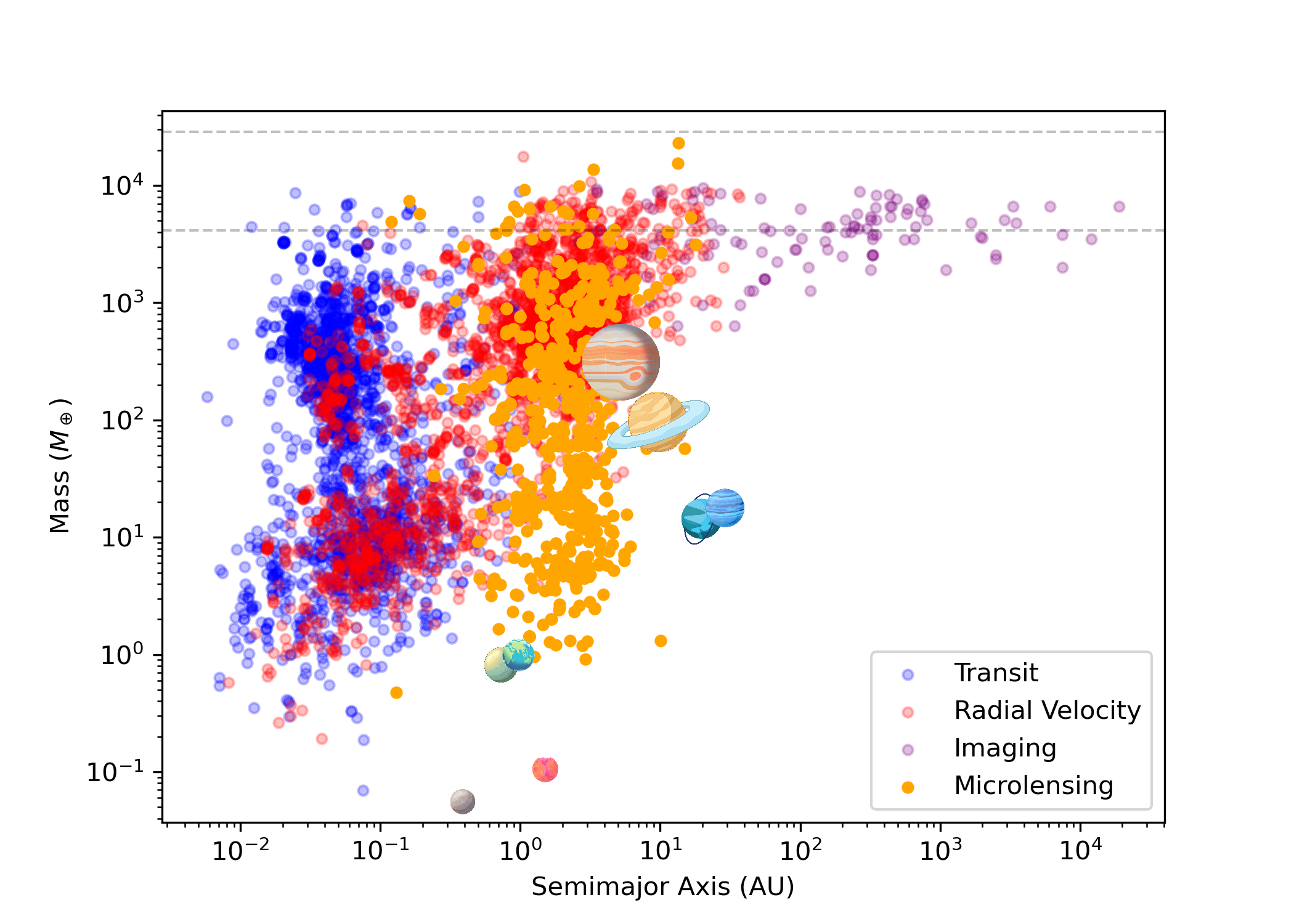
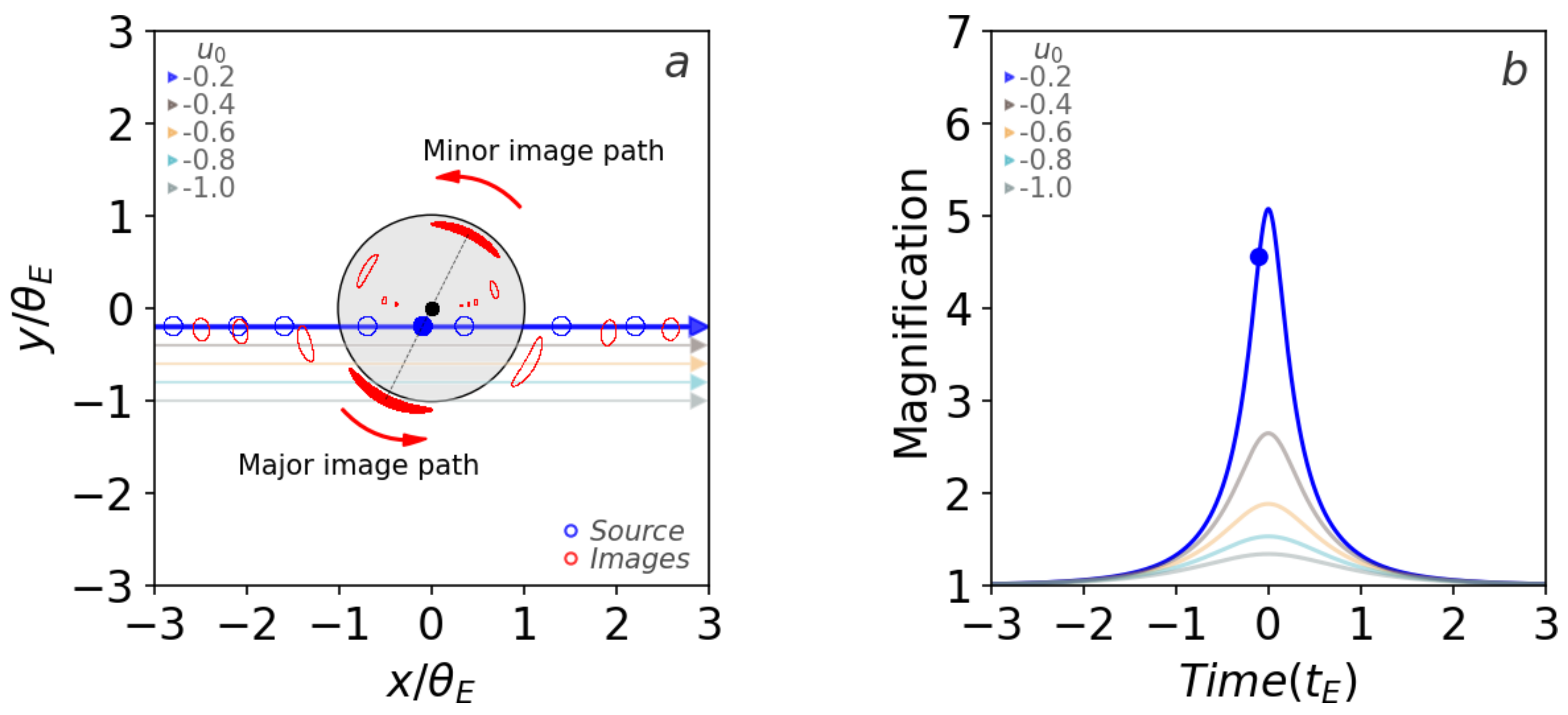
4. Lens Equation
The next chapters of the minicourse will cover the details of microlensing, and how this special case of gravitational lensing can be used to detect exoplanets. In preparation, we will cover here the lens equation, which helps to understand what is observed during a gravitational lensing event.
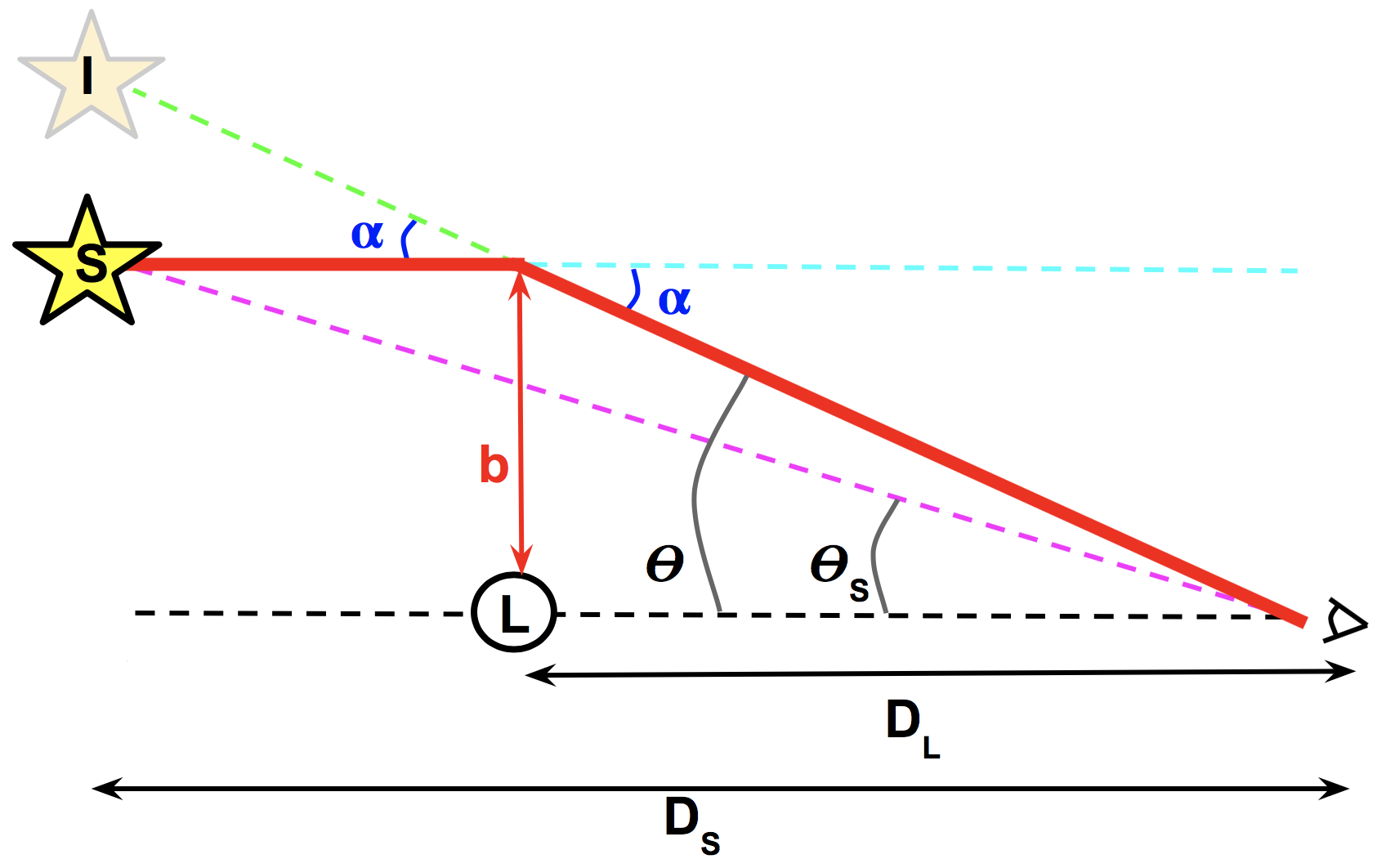
- θ = image position
- θS = background source position
- α = total deflection angle = θ
- DL = distance to lens
- DS = distance to source
- b = impact parameter
Lens Equation, continued

- From previous derivations: $$\alpha = \theta = \frac{4 G M}{b c^2}$$
- Small angle approximation: $$b = \theta D_L = \theta_S D_S$$
- Thus: $$\theta^2 = \frac{4 G M}{D_L c^2}, \theta\theta_S = \frac{4 G M}{D_S c^2}$$
Lens Equation, continued
Using the expressions for \(\theta^2\) and \(\theta\theta_S\), we define a characteristic angle for the system:
$$ \theta^2 - \theta \theta_S = \frac{4GM}{c^2} ( \frac{1}{D_L} - \frac{1}{D_s} ) = \frac{4GM}{c^2} \frac{D_S - D_L}{D_L D_S} $$This indeed defines the angle known as the Einstein Radius:
$$\theta_E = \sqrt{\frac{4 G M}{c^2}\frac{D_S - D_L}{D_L D_S}}$$Finally, we get the lens equation, which allows us to find the position of the lensed image, \(\theta\), in relation to the position of the source, \(\theta_S\), and the characteristic Einstein Radius of the lens, \(\theta_E\):
$$ \theta^2 - \theta\theta_S - \theta_E^2 = 0 $$Solving the Lens Equation
$$ \theta^2 - \theta\theta_S - \theta_E^2 = 0 $$We can solve the lens equation for \(\theta\) and determine the behavior of the lensing geometry for the following cases:
a) θS = 0
b) θS << θE
c) θS >> θE
Solving the Lens Equation, continued
As the lens equation is a quadratic equation, it has the following general solutions:
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$Solving the Lens Equation, continued
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$- $$a) \quad \theta_S = 0 \implies \theta = \theta_E$$
- Result: a perfect Einstein Ring

Solving the Lens Equation, continued
$$\theta = \frac{\theta_S \pm \sqrt{\theta_S^2 + 4\theta_E^2}}{2}$$- $$b) \quad \theta_S \ll \theta_E \implies \theta \approx \frac{\theta_S}{2} \pm \theta_E$$
- Result: If the source is inside the Einstein radius: Two images, one inside, one outside Einstein radius.
- $$c) \quad \theta_S \gg \theta_E \implies \theta \approx 0, \, \theta_S$$
- Result: If the source is far from the Einstein radius, you won't have lensing.